Les lumières : introduction

L'éclairage, comme dans le monde réel, ainsi que dans le cinéma, tient une place capitale dans le rendu des divers mondes en 3D que nous allons créer. Comme dans la plupart des domaines en informatique, nous allons arriver à nos fins à coups de calcul mathématiques, et ce pour le plus grand plaisir de nos yeux. Nous allons donc intégrer une notion supplémentaire au sein de la géométrie de nos objet, concernant la définition de nos points et nos triangles, qui est la notion de 'normale' à une face. Sans trop rentrer dans les détails pour le moment, le vecteur normal d'une face est en fait le vecteur représentant la perpendiculaire au plan formé par une face ou une surface donnée. Deuxième notion liée au normal face, chacun de ces vecteurs doit être normalisé (longueur comprise entre 0.0 et 1.0)

La lumière ambiante

La lumière ambiante correspond au modèle le plus simple. On considère qu'il existe une source lumineuse présente partout et qui éclaire de manière égale dans toutes les directions. Ce modèle de lumière correspond au niveau minimum d'éclairage qui sera appliqué sur les objets. En terme physique cela correspond un peu au soleil réfléchi par tout l'environnement qui donne une sorte de lumière présente partout. On définie l'intensité de cette lumière sur une surface comme suit : $Ip = pa*Ia$

Cette intensité lumineuse est constante sur toute la surface. 'Ia' désigne l'intensité de la lumière, 'pa' est le coefficient de réflexion de la lumière ambiante par la surface (0 <= pa <= 1). 'Ip' correspond à l'intensité de la lumière résultant de la réflexion sur la surface. Prenons un objet fait d'une matière unique. pa reste constant sur la totalité de l'objet. Dans ce cas, l'objet apparait d'une seule et même couleur. Ce modèle d'illumination ne met pas en valeur le volume d'un objet comme vous pouvez le voir sur la figure qui suit.

La réflexion diffuse

On prend maintenant comme hypothèse que la source de lumière est ponctuelle et qu'elle émet de manière constante dans toutes les directions de l'espace. Dans le modèle de réflexion diffuse, l'intensité en un point d'une surface dépend de l'angle formé entre le rayon de lumière qui touche le point de la surface et la normale à la surface. Plus l'angle formé entre le rayon de lumière et la normale au plan est faible, plus l'intensité lumineuse réfléchie visible par l'observateur est forte.

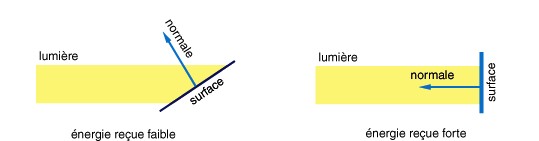
Le principe physique qui se cache derrière ce modèle est simple. Notre source lumineuse émet une certaine énergie au mètre carré. Suivant l'incidence des rayons lumineux, cette énergie sera répartie sur une plus ou moins importante surface de l'objet. Si les rayons et la surface sont perpendiculaires, alors l'énergie lumineuse sera répartie sur la plus petite surface possible et donc l'énergie par unité de surface sera maximale (voir figure).

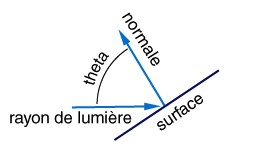
Maintenant, on sait pourquoi l'angle formé entre la normale au plan et les rayons de lumière est important. Par contre, on ne connait toujours pas la lumière qui sera réfléchie en direction de l'observateur. Pour cela on se base sur les propriétés de la surface. Si on considère que la surface est une surface Lambertienne (surface mate) comme le papier ou la neige, alors, on peut considérer que la lumière qui arrive sur la surface est réfléchie dans toutes les directions de manière égale. Dans ce cas, la position de l'observateur ne compte pas. La lumière émise en direction de l'observateur dépend donc de l'intensité de la source lumineuse, de l'angle theta formé par le rayon de lumière et la normale au plan et du coefficient de réflexion pd de la lumière diffuse par la surface (0 <= pd <= 1). On obtient la formule :  $Ip = pd * Il * cos(theta)$ Pour la figure :

On notera au passage que si theta est supérieur à PI/2 alors c'est que la face n'est pas du tout éclairée par la source lumineuse car elle lui tourne le dos. Dans ce cas, l'intensité lumineuse est 0. Voici un exemple de réflexion diffuse :

vec3 viewDir = normalize(-in_position);
vec3 lightDir = normalize(lightPosition - in_position);
vec3 diffuse = max(dot(in_normal, lightDir), 0.0) * lightData[lightIndex].lightColour.rgb;

La réflexion spéculaire

Le modèle de réflexion spéculaire se différencie du modèle de diffusion en faisant intervenir le point d'observation. Dans ce modèle les rayons de lumière sont réfléchis par symétrie par rapport à la normale à la surface. Ce modèle correspond aux propriétés de "miroir" des objets. Il faut calculer quel est le rayon réfléchi sur la face. Ensuite, l'intensité de la lumière observée dépend de theta qui correspond à l'angle entre le rayon réfléchi et le point d'observation, de l'intensité de la source de lumière et du coefficient de réflexion ps de la lumière spéculaire par la surface (0 <= ps <= 1). Si on se prend le rayon réfléchi dans l'oeil alors on a l'intensité maximum. Autour de cela, on peut quand même voir quelque chose d'un peu atténué. Cela veut dire que la surface ne réfléchit pas directement la rayon mais qu'il y a une certaine "diffusion" autour du rayon réfléchi. La fonction cosinus joue bien son rôle ici mais comme on veut pouvoir régler la diffusion autour du rayon réfléchi, on introduit le coefficient n. On obtient la formule $Is = ps * Il * cos(theta)^n$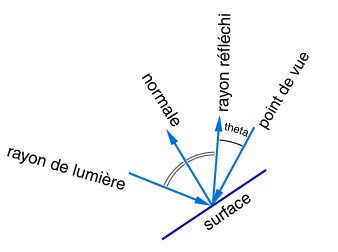




Voici un exemple de réflexion spéculaire :

vec3 halfDir = normalize(lightDir + viewDir);
float specPower = pow(max(dot(in_normal, halfDir), 0.0), 500.0);
vec3 specular = lightData[lightIndex].lightColour.rgb * specPower;