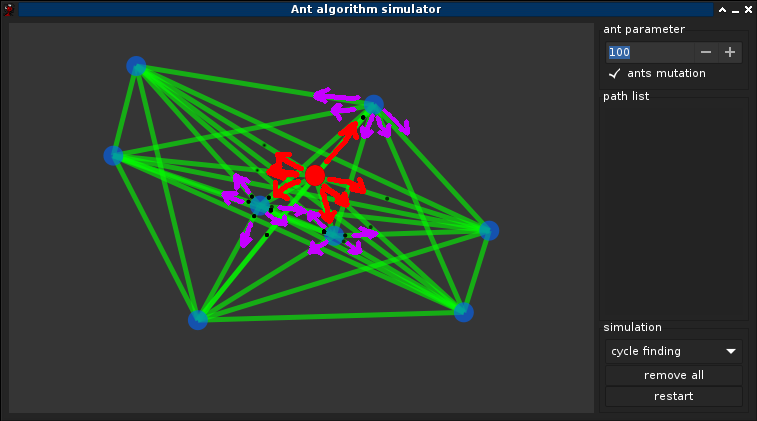
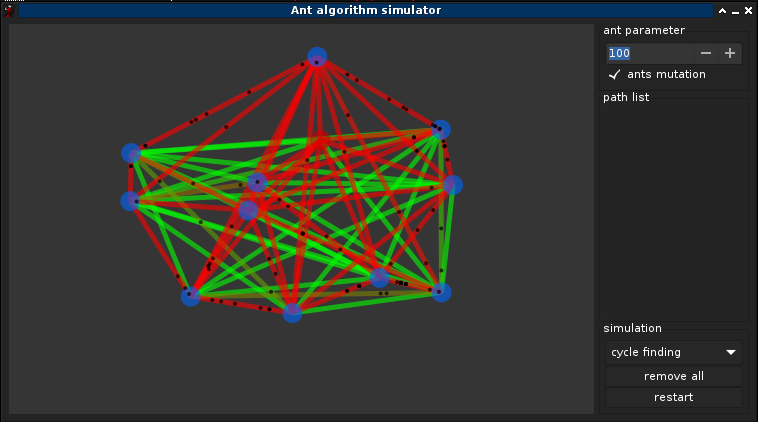
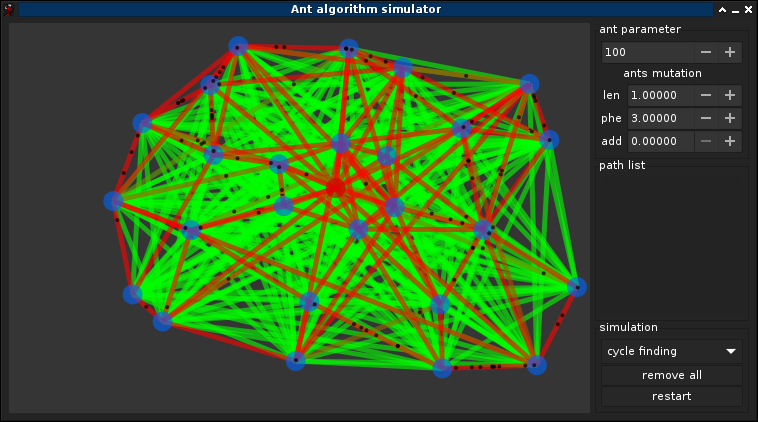
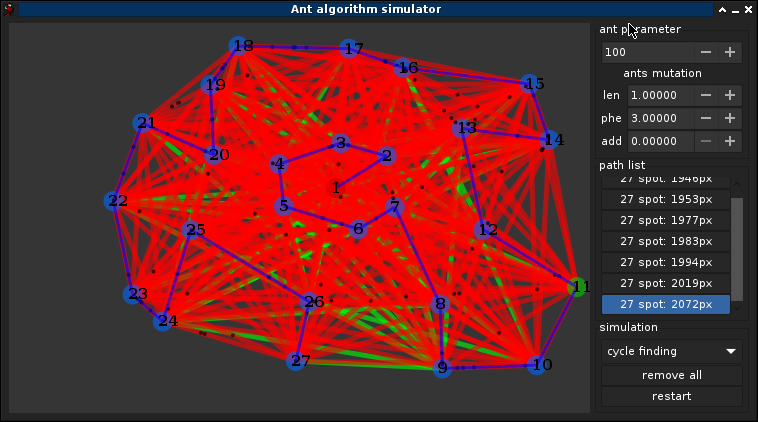
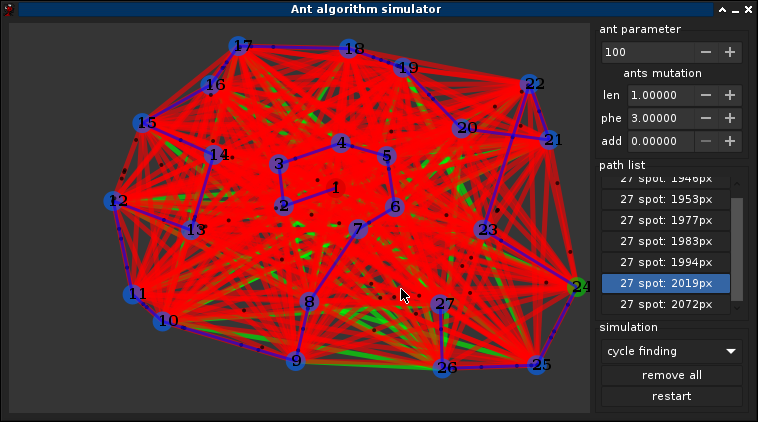
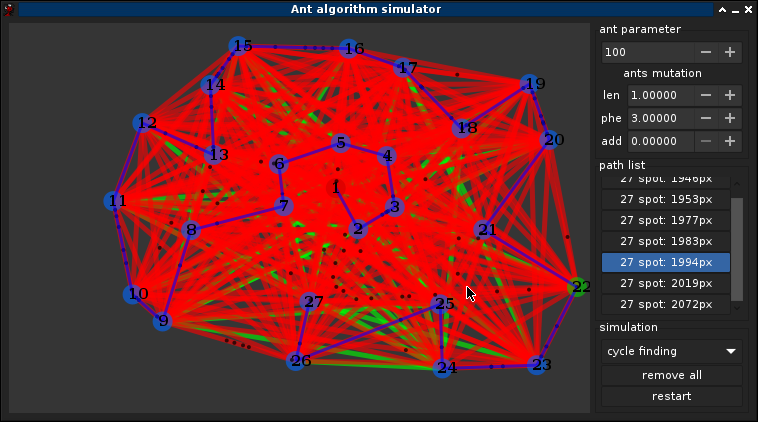
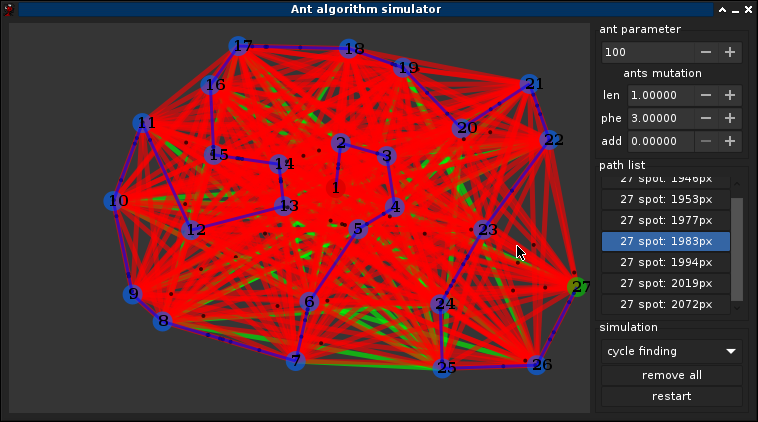
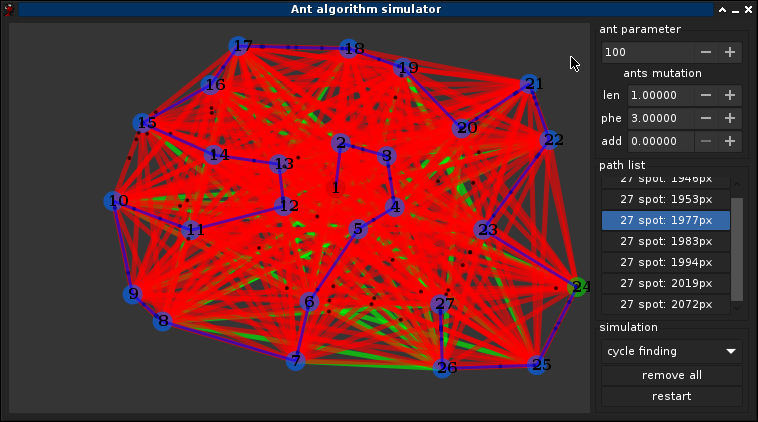
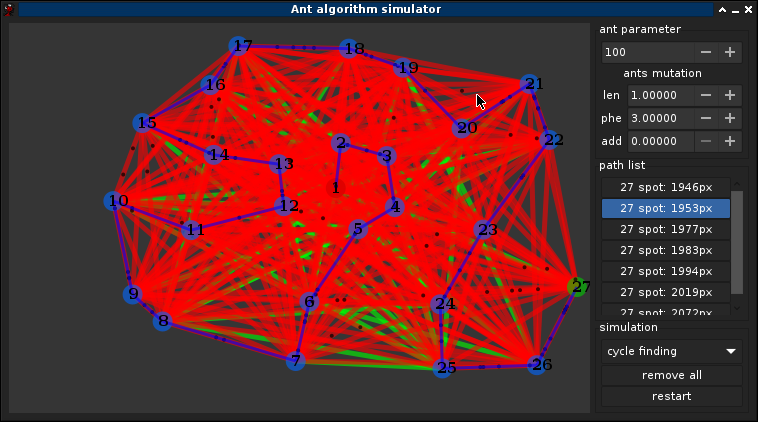
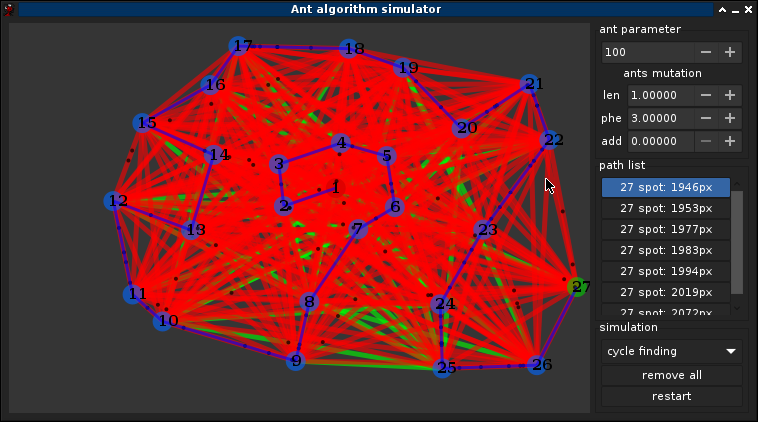
3.1°) Choix des paramètres
rapelle ω = aléatoire, α influent sur la longeur, β influent sur les phéromones
- lorsque le graph deviens trops grand (en nombre de noeud), et qu'il n'existe pas suffisament de fourmis pour avoire une convergence rapide vers une solution presque optimal alors ω premet d'augmenter le critère aléatoire sur le choix de l'arc, les fourmis peuvent donc empreinter plus souvent les arcs dont les phéromones et la longeurs sont normalement rejeter dans leurs contexte. ω doit être petit sinon la convergence n'apparait plus, bien que des solutions puissent émerger.
- lorsque les noeuds du graph sont très éloigner alors α a moins d'importance, dans ce cas priviligier α avec un ratio supérieur idéalement 10/(plus petite longueur / plus grand longeur). Et inverssement à ω, β doit être petit si le nombre de fourmis est inssufisent par rapport au nombre de noeud idéalement β peut être choisit par 3*(nombre de fourmis) / (nombre de ville)
Ses choix n'ont pas été l'objet d'étude pousser, mais seulement le fruit de constatation lors des expériences.
3.2°) Optimisation
Mutation des fourmis ! Si ω,α,β sont dépendant du graphe, or le graph n'ai pas nécéssairement connue a l'avance donc l'idée est de tendre vers une solution optmimal de ω,α,β pendant la simulation, une méthode simple est avisagable:
- valeurs par défault : ω=0 ; α=1; β=3
- α et β prenne des valeurs aléatoires dans [0;10] quand
- la fourmis ce perd (graph non complet) plus d'arc disponible
- la fourmis trouve un cycle avec une longueur > au chemain actuel
- ω ,α, β sont alors indépendants à chaque fourmis
cette solution simple montre après quelques teste, une convergance plus rapide vers une solution optimal (cf 6)
3.3°) Utilisation
| Clic gauche | Ajoute une ville |
| Clic droit sur un ville + déplacement | Ajoute un arc entre deux ville |
| Clic gauche + majuscule | Suprimme une ville |
| Clic droit + déplacement + majuscule | Suprimme un arc |
| Clic gauche + control | Ajoute une ville et des arcs vers chaque autres ville |
| Boutton “remove all” | Supprimme toutes les villes et tous les arcs |
| Button “restart” | Reinitialise les fourmis, phéromones |
| Molette souris vers le haut sur une ville | Définie la source de propagation et lance la propagation si simulation = “cycle finding” |
| Molette souris vers le bas sur une ville | Definie le point d'arriver pour la recherche de chemain (si simulation = “path finding”) et lance la simuluation dans ce cas |
| Ant parameter | Definie la quantiter de fourmis |
| Ant mutation (actif) |
|
| Ant mutation (inactif) : |
|
Source: svn://sleek-think.ovh/school/ant/
3.4°) Resultat expérimentaut
algorithme mise en oeuvre
| acceptable trouver après | meilleurs trouver après |
| 9.54s | 56.87s |
| 4.21s | 47.54s |
| 25.23s | 66.83s |
| 34.88s | 97.46s |
| 15.80s | 55.82s |
| 20.90s | 45.72s |
Algorithme avec mutation
| acceptable trouver après | meilleurs trouver après |
| 4.90s | 40.31s |
| 3.01s | 70.04s |
| 8.12s | 22.20s |
| 14.71s | 100.53s |
| 4.57s | 62.44s |
| 7.67s | 58.29s |
3.5°) Exemple complet
Pas d'autre solution trouver après (~40min) ont peut supposer que c'est une des meilleurs solutions, on peut également notifier que le graph ne change pas completements entre chaque itérations, les fourmis suivent toutes le chemin principale, le caractère aléatoire permet de trouver de fluctuer légèrement le chemin, bien quelles finissent par retrouver le chemin d'origine avec l'attirence des phéromones