Les lumières : introduction
Dans la création de mondes en 3D, l'éclairage revêt une importance fondamentale, tant dans la représentation fidèle du réel que dans celle du cinéma. Comme dans de nombreux domaines informatiques, nous atteindrons nos objectifs grâce à des calculs mathématiques, offrant ainsi une expérience visuelle optimale. Pour cela, nous introduirons un concept crucial dans la géométrie de nos objets : la notion de "normale" pour chaque face. En simplifiant, la normale d'une face est un vecteur perpendiculaire au plan qu'elle forme. De plus, chaque vecteur normalisé (avec une longueur comprise entre 0.0 et 1.0) garantira une représentation précise de la géométrie.
La lumière ambiante
La lumière ambiante constitue le modèle le plus élémentaire en matière d'éclairage. Il postule qu'il existe une source lumineuse omniprésente qui illumine de manière uniforme dans toutes les directions. Ce modèle représente le niveau minimal d'éclairage appliqué aux objets. Pour l'appréhender physiquement, on peut le comparer à la lumière solaire réfléchie par l'environnement, créant ainsi une sorte de luminosité diffuse. L'intensité de cette lumière sur une surface est définie par la formule : $Ip = pa*Ia$
Cette intensité lumineuse demeure constante sur toute la surface. Dans cette équation, 'Ia' représente l'intensité de la lumière ambiante, tandis que 'pa' correspond au coefficient de réflexion de la lumière ambiante par la surface $(0 <= pa <= 1)$. 'Ip' quantifie l'intensité de la lumière résultant de sa réflexion sur la surface. Imaginons un objet constitué d'une seule matière. Dans ce cas, 'pa' reste constant sur toute l'étendue de l'objet, ce qui donne à celui-ci une couleur uniforme. Cependant, ce modèle d'illumination ne parvient pas à mettre en relief le volume d'un objet, comme illustré dans la figure suivante.
La réflexion diffuse
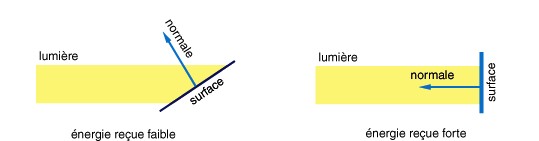
Dans le cadre de notre modèle, nous supposons désormais que la source lumineuse est ponctuelle et émet de manière uniforme dans toutes les directions de l'espace. Dans le contexte de la réflexion diffuse, l'intensité lumineuse en un point donné d'une surface dépend de l'angle formé entre le rayon de lumière incident touchant ce point et la normale à la surface. Plus cet angle est petit, c'est-à-dire plus le rayon lumineux est proche de la normale, plus l'intensité lumineuse réfléchie visible par l'observateur est forte.
Ce modèle repose sur un principe physique fondamental : notre source lumineuse émet une certaine quantité d'énergie par mètre carré. Selon l'angle d'incidence des rayons lumineux, cette énergie est répartie sur une surface de l'objet plus ou moins grande. Lorsque les rayons lumineux et la surface de l'objet sont perpendiculaires, l'énergie lumineuse est distribuée sur la plus petite surface possible, ce qui entraîne une concentration maximale d'énergie par unité de surface (voir figure).
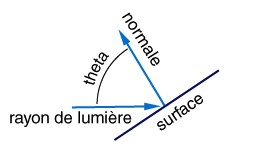
Maintenant que nous comprenons l'importance de l'angle entre la normale à la surface et les rayons lumineux, explorons comment déterminer la lumière qui sera réfléchie en direction de l'observateur. Pour cela, nous nous appuyons sur les propriétés de la surface. Si nous considérons que la surface est une surface lambertienne, telle que le papier ou la neige, alors nous pouvons postuler que la lumière incidente sur la surface est réfléchie de manière égale dans toutes les directions. Dans ce cas, la position de l'observateur n'a pas d'incidence. La lumière émise en direction de l'observateur dépend donc de l'intensité de la source lumineuse ('Il'), de l'angle theta formé par le rayon lumineux et la normale au plan, et du coefficient de réflexion 'pd' de la lumière diffuse par la surface $(0 <= pd <= 1)$. La formule obtenue est la suivante : $Ip = pd \times Il \times \cos(\theta)$. Voyons cela illustré dans la figure :

vec3 viewDir = normalize(-in_position);
vec3 lightDir = normalize(lightPosition - in_position);
vec3 diffuse = max(dot(in_normal, lightDir), 0.0) * lightData[lightIndex].lightColour.rgb;
La réflexion spéculaire
Le modèle de réflexion spéculaire se distingue du modèle de diffusion en intégrant le point d'observation. Dans ce schéma, les rayons lumineux sont réfléchis symétriquement par rapport à la normale à la surface. Ce modèle reflète les propriétés "miroir" des objets. Il implique le calcul du rayon réfléchi sur la surface, suivi de l'évaluation de l'intensité de la lumière perçue. Cette intensité dépend de theta, représentant l'angle entre le rayon réfléchi et le point d'observation, de l'intensité de la source lumineuse, et du coefficient de réflexion 'ps' de la lumière spéculaire par la surface (0 ≤ ps ≤ 1). Lorsque le rayon réfléchi est directement dans la ligne de vision, l'intensité est maximale. Autour de ce point, une certaine quantité de lumière peut encore être perçue, bien que légèrement atténuée. Cela indique que la surface ne reflète pas uniquement le rayon de manière directe, mais qu'il y a une diffusion autour de celui-ci. La fonction cosinus joue un rôle crucial ici, mais pour ajuster cette diffusion autour du rayon réfléchi, nous introduisons le coefficient 'n'. La formule obtenue est donc : $Is = ps * Il * cos(theta)^n$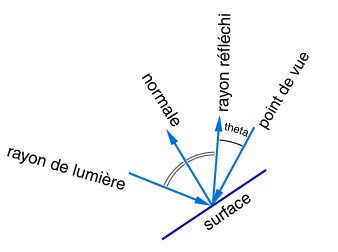
Voici un exemple de réflexion spéculaire :
vec3 halfDir = normalize(lightDir + viewDir);
float specPower = pow(max(dot(in_normal, halfDir), 0.0), 500.0);
vec3 specular = lightData[lightIndex].lightColour.rgb * specPower;
Atténuation de la lumière
Jusqu'à présent, la distance entre la source lumineuse et la surface n'a pas été prise en compte. Pour corriger cela, nous pouvons intégrer un coefficient d'atténuation de la lumière dans les modèles de réflexion diffuse et de réflexion spéculaire. Ce coefficient permet de pondérer l'intensité de la lumière en fonction de la distance. Voici un exemple de coefficient de pondération : $fd = min(1/(c1+c2*dist+c3*dist^2), 1)$
float attenuation = 1.0 - clamp(dist / lightData[lightIndex].lightRadius, 0.0, 1.0);
attenuation *= lightData[lightIndex].intensity;
Pour éviter que l'atténuation ne devienne une amplification, nous prenons le minimum entre 1 et la valeur calculée. Cette formule introduit trois nouveaux coefficients sur lesquels nous pouvons agir. Pour l'utiliser dans les modèles de réflexion mentionnés précédemment, nous devons d'abord calculer la distance entre la source lumineuse et le point où nous évaluons l'intensité lumineuse. Ensuite, nous calculons la lumière selon le modèle choisi, en appliquant également le coefficient $f_d$. Le résultat final de l'intensité lumineuse est obtenu en multipliant l'intensité calculée par le coefficient d'atténuation $f_d$.
Modèle de lumière complexe
Pour obtenir des illuminations plus complexes, nous combinons la lumière spéculaire avec la lumière diffuse et la lumière ambiante, tout en tenant compte du coefficient de pondération en fonction de la distance. Pour ce faire, il suffit de calculer les intensités d'illumination pour chacun de ces modèles et d'additionner les résultats pour obtenir l'intensité lumineuse totale. De la même manière, si nous voulons intégrer plusieurs sources de lumière dans une scène, il nous suffit de calculer l'intensité lumineuse pour chaque source sur une surface donnée, puis d'additionner toutes les intensités pour obtenir l'intensité résultante de l'ensemble des sources de lumière sur cette surface.
Utilisation de l'intensité
En général, un point sur un écran (pixel) est représenté par trois composantes : le rouge, le vert et le bleu. Prenons l'exemple de la couleur marron, décomposée en 165 de rouge, 42 de vert et 42 de bleu. Supposons que nous ayons calculé une intensité de 0.7 pour ce point marron. Pour obtenir la nouvelle teinte de marron correspondant à une intensité de 0.7, il suffit de multiplier les composantes rouge, verte et bleue du marron initial par cette intensité. Ainsi, nous obtenons : 115 pour le rouge, 29 pour le vert et 29 pour le bleu.
Cela nous conduit à une autre question : les valeurs de rouge, de vert et de bleu sur un écran (dans la mémoire vidéo) sont bornées. Si nous considérons que ces valeurs sont comprises entre 0 et 255, que se passe-t-il en cas de débordement ? Par exemple, si l'intensité lumineuse en un point est importante (par exemple, 8), et que les valeurs dépassent 255, nous pouvons simplement plafonner les valeurs à 255. Bien que cela ne corresponde pas à un modèle physique précis, cela peut simuler un effet d'éblouissement où tout devient blanc lorsque la lumière est trop forte.
Voici un exemple qui illustre l'application de cette saturation en utilisant la lumière ambiante, la réflexion diffuse et spéculaire :
Les modèles d'ombrage
Maintenant que nous savons comment calculer l'intensité lumineuse en un point, nous nous heurtons souvent à des contraintes de performances. En effet, la plupart du temps, il n'est pas réaliste de calculer la lumière pour chaque point de la scène. De plus, la plupart des logiciels 3D modélisent les objets à l'aide de polygones, ce qui signifie que l'objet final ne sera pas nécessairement constitué de faces planes. Il est peu pratique, voire impossible, d'utiliser un nombre infini de faces plates pour représenter des objets courbes. Cependant, même dans ce cas, il est important de conserver un aspect courbé réaliste. Pour cela, plusieurs techniques d'approximation de la lumière en un point sont couramment utilisées. Nous allons explorer les plus courantes.
L'ombrage plat
Commençons par la méthode la plus simple : l'ombrage plat. Cette méthode consiste à calculer la lumière pour un seul point de la surface que nous souhaitons représenter, puis à utiliser la même intensité pour l'ensemble de la surface. Bien que cette méthode soit simple, elle a tendance à mettre fortement en évidence les polygones qui composent un objet.
L'ombrage de Gouraud
L'ombrage de Gouraud repose sur le calcul de l'intensité lumineuse aux sommets du polygone, puis sur une interpolation linéaire de ces intensités pour déterminer l'intensité lumineuse en chaque point de la face. Cette interpolation linéaire s'effectue le long des arêtes du polygone projeté. Cette technique permet d'obtenir un rendu plus lisse qui atténue les frontières visibles entre les polygones générées par l'ombrage plat. Voici un exemple illustrant le remplissage avec l'ombrage de Gouraud :
L'ombrage de Phong
L'ombrage de Phong partage des similitudes avec l'ombrage de Gouraud, mais avec une différence significative : au lieu d'interpoler linéairement les intensités lumineuses des sommets sur le polygone 3D, on interpole les normales des sommets. Comme nous l'avons vu précédemment, pour calculer l'intensité lumineuse en un point, notamment dans les modèles de diffusion et de spécularité, nous avons besoin de la normale à la surface en ce point.
Avec l'ombrage de Phong, nous interpolons linéairement les normales des sommets pour obtenir une normale en chaque point, puis utilisons cette normale pour recalculer l'intensité lumineuse en chaque point. Il est évident que cette méthode est plus coûteuse en termes de calcul que l'ombrage de Gouraud, mais elle offre un meilleur rendu du modèle d'illumination spéculaire tout en utilisant un nombre moindre de polygones.
En effet, dans certains cas, la zone éclairée peut être petite voire entièrement contenue dans un polygone. Dans cette situation, si nous calculons les intensités lumineuses aux sommets, elles ne seront pas représentatives de l'éclairage au centre de la zone éclairée. Avec l'ombrage de Gouraud, cette variation ne serait pas visible, tandis qu'avec l'ombrage de Phong, elle serait prise en compte car la lumière est recalculée en chaque point (même si c'est avec une normale interpolée). La plupart des illustrations des modèles d'illumination sont réalisées avec l'ombrage de Phong. Voici un exemple démonstratif du remplissage avec l'ombrage de Phong :

Les différents type de lights
![]()
Les lumières, sous forme de "nodes", exercent leur influence sur les objets 3D, comme nous l'avons vu précédemment. En informatique, elles peuvent être classées en deux grandes catégories :
1. Lumières Ambiantes:
Une lumière ambiante, comme rappelé précédemment, est si dispersée qu'elle perd toute directionnalité et source identifiable. Elle illumine chaque point de la scène avec une intensité uniforme. Définie par sa couleur et son intensité, elle ne contribue à aucune réflexion spéculaire et agit indépendamment des autres lumières présentes dans la scène. En termes de calculs, c'est la moins coûteuse parmi tous les types de lumières.
2. Lumières directionnelles:
Point

vec3 pointLightDirection(Light light, vec3 position) {
return normalize(light.point.position - position);
}
float pointLightAttenuation(Light light, vec3 position) {
float d = length(light.point.position - position);
float attenuation = light.point.attenuation.constant +
light.point.attenuation.linear * d +
light.point.attenuation.quadratic * d * d;
return 1 / attenuation;
}
Directionelle
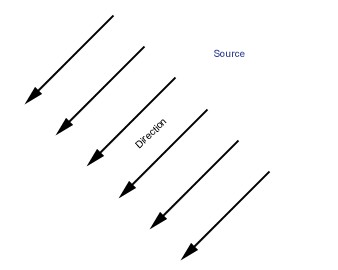
vec3 directionalLightDirection(Light light, vec3 position) {
return -light.directional.direction;
}
float directionalLightAttenuation(Light light, vec3 position) {
return 1.0f;
}
Spot

vec3 spotLightDirection(Light light, vec3 position) {
return normalize(light.spot.position - position);
}
float spotLightAttenuation(Light light, vec3 position) {
vec3 dir = normalize(light.spot.direction);
float d = length(light.spot.direction);
float attenuation = light.spot.attenuation.constant +
light.spot.attenuation.linear * d +
light.spot.attenuation.quadratic * d * d;
vec3 l = normalize(light.spot.position - position);
float cosRealAngle = dot(l, dir);
float cosSpotOuter = cos(light.spot.innerAngle / 2.0);
float radialAttenuation = pow(clamp((cosRealAngle - cosSpotOuter) / (1.0 - cosSpotOuter), 0.0, 1.0), 1.6);
return radialAttenuation / attenuation;
}
