Réallignement d'images multi-spectral
L'enregistrement des images est le processus qui consiste à transformer différentes images d'une scène dans un même système de coordonnées. Les relations spatiales entre ces images peuvent être rigides (translations et rotations), affines (cisaillements par exemple), homographiques, ou de modèles plus complexes de déformation (en raison de la différence de profondeur entre le sol et les feuilles par exemple). La principale difficulté est que les caméras multispectrales ont une faible couverture spectrale entre les bandes :
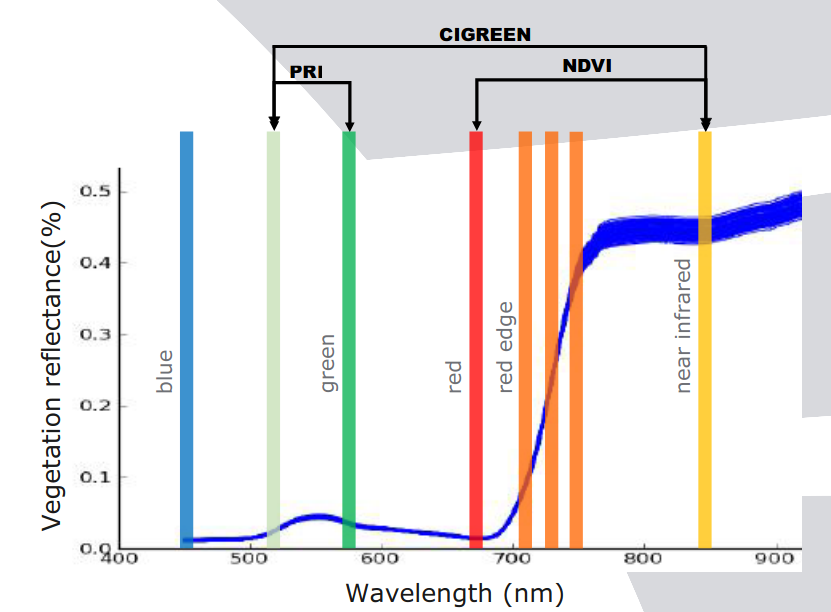
ce qui entraîne une perte de caractéristiques communes entre elles. Cela est dû au fait que :
- les feuilles des plantes ont un aspect différent selon les bandes spectrales
- par exemple valeur haute dans le proche infra-rouge et basse dans le bleu
- nos images présentent des structures très complexes et auto-similaires
- effectivement ont retrouve les "mêmes" feuilles partout dans l'image
- idem pour le sol et d'éventuelles cailloux
Cela affecte donc le processus de détection de caractéristiques communes entre les bandes pour l'enregistrement des images. Il existe deux types d'enregistrement, basé sur des points-clé ou sur l'intensité.
- Les méthodes basées sur les points-clé fonctionnent en extrayant des points d'intérêt et en utilisant la correspondance de caractéristiques (texture). Dans la plupart des cas, une mise en correspondance par bruteforce est utilisée (teste toutes les combinaisons), ce qui rend ces techniques lentes. Heureusement, ces points-clé peuvent être filtrées sur des propriétés spatiales pour réduire le nombre de correspondance à effectuer.
- L'enregistrement basé sur l'intensité est un processus itératif, et les métriques utilisées sont difficile à définir et influence le nombre d'itérations, ce qui rend ce genre de méthode coûteuse en termes de calcul pour un enregistrement précis. En outre, le multispectral implique des métriques différentes pour chaque bande enregistrée, ce qui est difficile à réaliser.
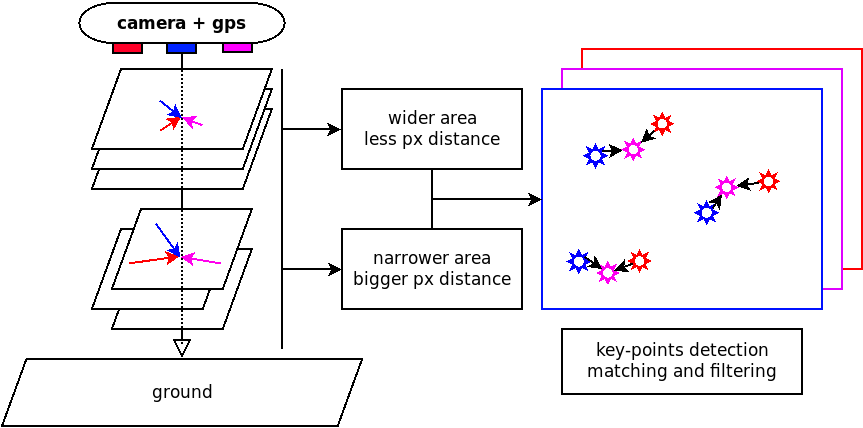
On peut trouver différentes études d'alignement d'images à l'aide de caméras multi-capteurs pour l'acquisition par drones à des distances moyennes (50-200 m) et élevées (200-1000 m). Certaines montrent de bonnes performances (en termes de nombre de points clés) avec une forte recherche sur l'amélioration des descripteurs de ces points clé. D'autres préfèrent utiliser un enregistrement basé sur l'intensité avec de meilleures mesures de convergence (en termes de corrélation), ce qui est plus lent et pas nécessairement robuste contre la variabilité de la lumière et leurs optimisations peuvent également tomber dans un minimum local, ce qui entraîne un enregistrement non optimal.
L'approche traditionnelle de l'enregistrement d'images multispectrales consiste de plus à désigner un canal de référence et à déplacer tous les autres vers le canal sélectionné. Actuellement, seule un article [Dantas Dias Junior 2019] propose une méthode de sélection de la meilleure référence, mais aucune étude n'a été menée pour déterminer exactement la quel est la meilleure référence spectrale dans une scène agronomique. Dans tous les cas, le proche infrarouge (850 nm) ou la référence spectrale de moyenne gamme sont utilisés de manière conventionnelle sans étudier les autres (particulièrement en agriculture de précision). En outre, ces études proposent principalement des méthodes basé sur la mises en correspondances de points clé sans grande comparaison des algorithmes de détection de ces points clé (moins de 4). Ces études ne propose pas non plus d'informations sur les performances (temps/précision). Et ne montre pas non plus l'importance de la référence spectrale à utiliser, tout comme l'intérêt de travailler dans le domaines des gradients (comme dans les méthodes basées sur l'intensité). Tout cela seras donc l'objectif de ce billet.
Objectif
La méthode proposer repose sur un alignement affiné en deux étapes, avec :
- l'enregistrement affine approximativement estimé
- l'enregistrement perspective pour l'affinement et la précision.
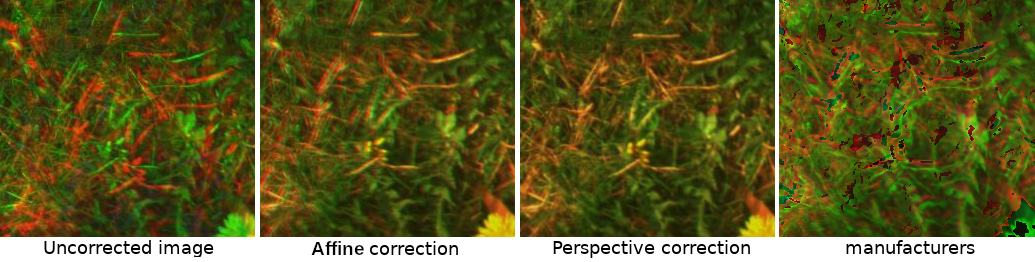
À titre d'exemple, la figure suivante montre chaque étape de correction, où la première ligne est pour la (1) correction affine, la seconde pour la (2) correction en perspective. Plus précisément, la deuxième étape est un prétraitement par canal où des algorithmes détection de points clés sont utilisés. Les points clés de chaque canal sont associés pour calculer la correction de perspective en cherchent une homographie vers la bande spectrale de référence. Ces étapes sont expliquées dans les sections suivantes.
Ainsi, cette étude propose un benchmark des algorithmes de détection de points populaire appliqué au domaine des gradients. De plus la meilleure référence spectrale a été définie pour chacun d'entre eux. Nous allons aussi définir dans un premier temps un enregistrement affine utilisé dans la seconde étapes pour filtrer la correspondance des points-clés, évaluées à différentes résolutions spatiales. Cette étude montre donc l'importance de la sélection de la référence et de l'extracteur de points-clé sur des gradients.
Cette session à fait l'objet d'article présenter dans la conférence VISAPP à Malte
Matériel et données

L'imagerie multispectrale a été fournie par la caméra multispectrale disposant de six bandes Airphen. C'est une caméra multispectrale scientifique développée par des agronomes pour des applications agricoles. Elle peut être embarquée dans différents types de plateformes telles que des drones, des robots de phénotypage, etc. Elle est hautement configurable (bandes, champs de vision), légère et compacte. Elle peut fonctionner sans fil et être combiné avec des caméras infrarouges thermiques complémentaires et des caméras RVB haute résolution.
- La caméra a été configurée en utilisant des filtres centré sur 450/570/675/710/730/850 nm avec une FWHM de 10nm.
- Chaque lentille à une focal de 8mm.
- La résolution des images sont de 1280x960 px avec une précision de 12 bits.
- Une antenne GPS interne est disponible pour le géoréférencement
Deux séries de données ont été prises à des hauteurs différentes (1,6 à 5,0 mètres avec une pente de 20 cm).
- Pour l'étalonnage, un échiquier est pris à une hauteur différente
- Pour la vérification de l'alignement, des clichés de la prairie est pris à différentes hauteurs

Correction affine
Nous allons faire l'hypothèse que plus on se rapproche du sol, plus la distance de la correction affine initiale est grande. En revanche, à une distance supérieure ou égale à 5 mètres, la correction affine initiale est proche de quelques pixels (1-5), ce qui est suffisant pour prendre une matrice d'identité.
Calibration : Sur la base de cette hypothèse précédente, un étalonnage est effectué sur l'ensemble des données de l'échiquier. Nous détectons l'échiquier en utilisant la toolbox de calibration opencv sur chaque image spectrale à différentes hauteurs (de 1,6m à 5m). Ont s'aide de la fonction findChessboardCorners qui tente de déterminer si l'image d'entrée est une vue du motif d'échiquier et localise les coins internes de ce dernier. Les coordonnées détectées sont approximatives. Pour déterminer leurs positions avec précision, nous utilisons la fonction cornerSubPix comme expliqué dans la documentation :
for x in range(len(height)):
h = height[x]
S = SpectralImage()
imgpoints = [None] * len(bands)
for s,i in enumerate(bands):
image = S.read_tiff(directory + h + str(i) + 'nm.tif')
image = np.clip(image / image.max() * 255, 0, 255)
image = image.astype('uint8')
ret, corners = cv2.findChessboardCorners(image, chessboard_shape, None)
if ret == True:
corners2 = cv2.cornerSubPix(image, corners, chessboard_shape, (-1,-1), criteria)
imgpoints[s] = corners2
Les données doivent être organisé puisque la détection du chessboard peut dans certain cas être "retourné" :
imgpoints = np.array(imgpoints)
for i in range(imgpoints.shape[0]):
imgpoints[i] = imgpoints[i, np.argsort(imgpoints[i,:,0,0]), :, :]
imgpoints[i] = imgpoints[i, np.argsort(imgpoints[i,:,0,1]), :, :]
np.save('data/' + h[0:-1] + '.npy', imgpoints)
Modèle linéaire : En utilisant tous les points détectés pour chaque bande spectrale, ont peu calculer un « grille centrale » (moyenne de chaque point). La transformée affine de chaque bande spectrale vers cette « grille centrale » est estimée. Théoriquement, la rotation et l'échelle ($A,B,C,D$) ne dépendent pas de la distance au sol, mais la translation ($X,Y$) oui. Les données extraites sont alors les suivantes et semble respecter notre assertion de départ :


Ainsi, un algorithme d'ajustement de courbe (Levenberg-Marquardt) avec régression linéaire des moindres carrés peut être utilisé pour ajuster une équation pour chaque bande spectrale par rapport à $X$ et $Y$ indépendamment vers cette « grille centrale ». Nous ajustons donc l'équation suivante $t = \alpha h^3 + \beta h^2 + \theta h + \gamma$ où $h$ est la hauteur, $t$ est la translation résultante et les facteurs $\alpha,\beta,\theta,\gamma$ sont les paramètres du modèle, ce qui correspond à la fonction $polynomial\_curve(x,a,b,c,d)$. Cela correspond plus spécifiquement au code suivant :
from scipy.optimize import curve_fit
def polynomial_curve(x, a, b, c, d):
return a*x**3 + b*x**2 + c*x + d
# exemple pour l'ajustement de courbe entre $x$ et $h$
for i in range(all_transform_x.shape[1]):
x, y = height, all_transform_x[:,i]
popt, pcov = curve_fit(polynomial_curve, x, y)
Ont peu alors visualiser l'apprentissage de ces courbes en positionnant les points de détection et les courbes polynomial correspondantes :
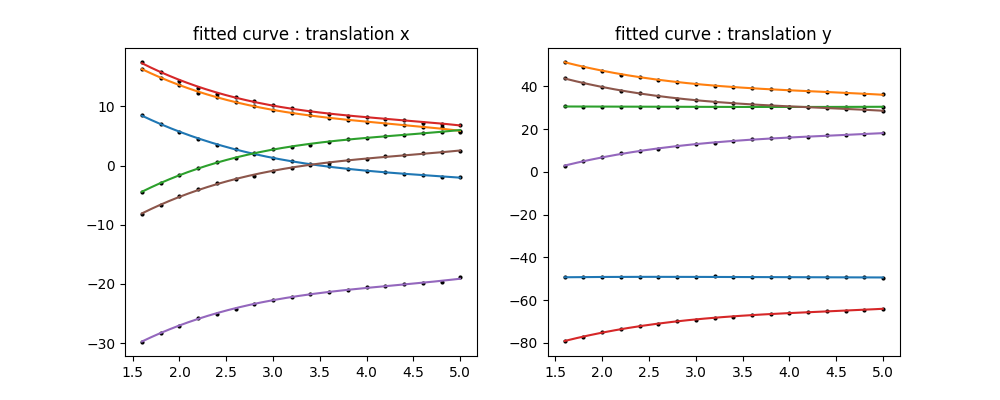
Correction : Sur la base du modèle estimé sur l'ensemble des données de l'échiquier, nous les transposons alors à l'ensemble des images de prairie. Pour effectuer la correction matricielle affine, nous utilisont les facteurs ($A,B,C,D$) de rotation et d'échelle à la hauteur la plus précise (1,6m la où la résolution spatiale de l'échiquier est la plus élevée), car elle ne dépend théoriquement pas de la hauteur. Pour la partie translation ($X,Y$), le modèle de courbe est appliqué pour chaque bande spectrale en utilisant la hauteur donnée fournie par le GPS de la caméra ! Chaque bande spectrale est déformée à l'aide de la transformation affine correspondante. Enfin, toutes les bandes spectrales sont recadrées à la limite minimale (translation minimale et maximale de chaque matrice affine). Cette première correction est une approximation du faite de l'imprécision du GPS. Elle fournit néhanmoins certaines propriétés spatiales que nous utiliserons lors de la deuxième étape !!
def affine_transform_linear(S, loaded):
dsize = (loaded[0].shape[1], loaded[0].shape[0])
transform = [None] * len(loaded)
# best factor $a,b,c,d$ for each spectral band
# extracted from the calibration
rotation_scale = [(A,B,C,D) * len(bands)]
# idem for $alpha,beta,gamma,psi$ on each spectral band
translation_model_params = [(X_params,Y_params) * len(bands)]
for i in range(len(loaded)):
x = polynomial_curve(S.height, *translation_model_params[i][0])
y = polynomial_curve(S.height, *translation_model_params[i][1])
transform[i] = np.array([
[rotation_scale[i][0], rotation_scale[i][1], x],
[rotation_scale[i][2], rotation_scale[i][3], y],
])
loaded[i] = cv2.warpAffine(loaded[i], transform[i], dsize)
return loaded, np.array(transform)Résultat affine

Correction perspective
Chaque bande spectrale a des propriétés et des valeurs différentes par nature, mais nous pouvons essayer d'extraire des similaritées en transformant chaque bande spectrale vers une dérivée absolue, pour trouver des similarités dans la rupture des gradients entre elles et tout particulièrement sur les bordures des feuilles ! Comme nous pouvons le voir sur la figure suivante, les gradients peuvent avoir des directions opposées selon les bandes spectrales, ce qui fait de la dérivée absolue une étape importante pour la correspondance entre les différentes bandes spectrales. Passer l'information en absolue permet d'obtenir des gradient dans le "même" sens.
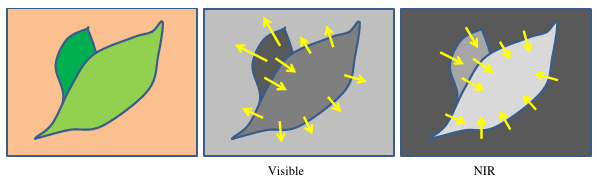
La correction affine permet de faciliter la recherche et la mise en correspondance de points-clé en ajoutant les propriétés des lignes épipolaires (proche). Ainsi, la correspondance de points-clé extraits peut être spatialement délimitée car nous savons que :
- la translation entre deux point-clés est limitée à quelques pixels (moins de 10px grâce à la correction affine)
- l'angle entre deux point-clés est limité à $[-1,1]$ degré (la rotation est infime)
- idem pour la mise à l'échelle qui est proche de zero
Calcule des gradients : Pour calculer le gradient de l'image avec un impact minimal de la distribution lumineuse (bruit, ombre, réflectance, spéculaire, ...), chaque bande spectrale est normalisée en utilisant le flou gaussien, la taille du noyau est fixé empiriquement à 19 et les images normalisées finales sont définies par $I/(G+1)*255$ où $I$ est la bande spectrale et $G$ est le flou gaussien de ces bandes spectrales. Cette première étape permet de minimiser l'impact du bruit sur le gradient et de lisser le signal en cas de forte réflectance. En utilisant cette image normalisée, le gradient $I_{grad}(x,y)$ est calculé avec la somme absolue des filtres de Sharr pour la dérivée horizontale $S_x$ et verticale $S_y$, notée $I_{grad}(x,y)=\frac{1}{2}|S_x|+\frac{1}{2}|S_y|$. Enfin, tous les gradients $I_{grad}(x,y)$ sont normalisés à l'aide de CLAHE pour améliorer localement leur intensité et augmenter le nombre de points clés détectés. Ont transpose donc tout cela en code python :
def build_gradient(img, scale = 0.15, delta=0):
clahe = cv2.createCLAHE(clipLimit=1.0, tileGridSize=(8,8))
grad_x = cv2.Scharr(img, cv2.CV_32F, 1, 0, scale=scale, delta=delta, borderType=cv2.BORDER_DEFAULT)
grad_y = cv2.Scharr(img, cv2.CV_32F, 0, 1, scale=scale, delta=delta, borderType=cv2.BORDER_DEFAULT)
abs_grad_x = cv2.convertScaleAbs(grad_x)
abs_grad_y = cv2.convertScaleAbs(grad_y)
grad = cv2.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0)
grad = cv2.convertScaleAbs(grad)
grad = grad.astype('float')**2
grad = grad/grad.max()*255
grad = grad.reshape([*grad.shape, 1])
grad = grad.astype('uint8')
grad = clahe.apply(grad)
return grad.astype('uint8')Extracteur de points clé : Un point clé est un point d'intérêt. Il définit ce qui est important et distinctif dans une image (coins, bords, etc.). Différents types d'extracteurs de points clés ont été testé. Ces algorithmes sont largement décrits dans de multiples études, ils sont tous disponibles et facilement utilisables grâce à OpenCV. Nous allons donc les étudiées en faisant varier les paramètres les plus influents pour chacune d'entre elles avec trois modalités :
| Abrv | paramètre | modalité 1 | modalité 2 | modalité 3 |
| ORB | nfeatures | 5000 | 10000 | 15000 |
| AKAZE | nOctaves, nOctaveLayers | (1, 1) | (2, 1) | (2, 2) |
| KAZE | nOctaves, nOctaveLayers | (4, 2) | (4, 4) | (2, 2) |
| BRISK | nOctaves, nOctaveLayers | (0, 0.1) | (1, 0.1) | (2, 0.1) |
| AGAST | threshold | 71 | 92 | 163 |
| MSER | None | None | None | None |
| SURF | nOctaves, nOctaveLayers | (1, 1) | (2, 1) | (2, 2) |
| FAST | threshold | 71 | 92 | 163 |
| GFTT | maxCorners | 5000 | 10000 | 15000 |
def keypoint_detect(img1, img2, method='GFTT'):
# dictionnaire contenant les différent algos
# cf tableau précédent
detectors = {'ORB' : None}
# construction du detecteur de point clé
detector = detectors[method]()
# detection des points clé
kp1, kp2 = detector.detect([img1, img2],None)
# construction du modél d'extraction de propriété
descriptor = cv2.ORB_create()
# extraction de proriété par point-clé
(kp1, kp2), (des1, des2) = descriptor.compute([img1, img2], [kp1, kp2])
# association par bruteforce (toute les combinaisons)
bf = cv2.BFMatcher(descriptor.defaultNorm(), crossCheck=True)
# association
matches = bf.match(des1,des2)
return matches, kp1, kp2
Détection de point clé : Nous utilisons un des extracteurs de points clés mentionnés ci-dessus entre chaque gradient de bande spectrale (tous les extracteurs sont évalués). Pour chaque point clé détecté, nous extrayons un descripteur en utilisant le descripteur de texture de ORB. Nous faisons correspondre tous les points clés détectés vers la bande spectrale de référence (toutes les bandes sont évaluées). Toutes les correspondances sont filtrées par distance, position et l'angle, afin d'éliminer la majorité des faux positifs le long des lignes épipolaires correspondantes. Enfin, nous utilisons la fonction findHomography entre les points clés détectés/filtrés avec le RANSAC, pour déterminer le meilleur sous-ensemble de correspondances afin de calculer la correction de perspective.
def refine_allignement(loaded, method='SURF', ref=1, verbose=True):
img = [ i.astype('float32') for i in loaded]
img = [ gradient_normalize(i) for i in img]
grad = [ build_gradient(i).astype('uint8') for i in img]
img = [ (i/i.max()*255).astype('uint8') for i in img]
# identify transformation for each band to the next one
dsize = (loaded[0].shape[1], loaded[0].shape[0])
bbox, centers, keypoint_found = [], [], []
max_dist = 10
for i in range(0, len(loaded)):
if i == ref:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
matches, kp1, kp2 = keypoint_detect(grad[ref], grad[i], method)
matches = keypoint_filter(matches, kp1, kp2, max_dist)
if len(matches) < 2:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
source = np.array([kp1[i.queryIdx].pt for i in matches], dtype=float)
target = np.array([kp2[i.trainIdx].pt for i in matches], dtype=float)
matches = [cv2.DMatch(i,i,0) for i in range(len(source))]
source = source[np.newaxis, :].astype('int')
target = target[np.newaxis, :].astype('int')
M, mask = cv2.findHomography(target, source, cv2.RANSAC)
if M is None:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
loaded[i] = cv2.warpPerspective(loaded[i], M, dsize)
bbox.append(get_perspective_min_bbox(M, loaded[ref]))
center = np.array(dsize)/2
centers.append(cv2.perspectiveTransform(np.array([[center]]),M)[0,0] - center)
mask = np.where(mask.flatten())
target = np.float32(target[0,mask,:])
source = np.float32(source[0,mask,:])
keypoint_found.append(len(mask[0]))
return loaded, np.array(bbox), keypoint_found, np.array(centers)Correction : La correction de perspective entre chaque bande spectrale et la référence est estimée et appliquée. Enfin, toutes les bandes spectrales sont recadrées à la limite minimale, obtenue en appliquant une transformation de perspective à chaque coin de l'image (plus un offset $p$) :
def get_perspective_min_bbox(M, img, p=2):
h,w = img.shape[:2]
pts_x = np.float32([[ p, p], [ p, h-p]]).reshape(-1,1,2)
pts_y = np.float32([[w-p,h-p], [w-p, p]]).reshape(-1,1,2)
coords_x = cv2.perspectiveTransform(pts_x,M)[:,0,:]
coords_y = cv2.perspectiveTransform(pts_y,M)[:,0,:]
[xmin, xmax] = max(coords_x[0,0], coords_x[1,0]), min(coords_y[0,0], coords_y[1,0])
[ymin, ymax] = max(coords_x[0,1], coords_y[1,1]), min(coords_x[1,1], coords_y[0,1])
return np.int32([ymin,xmin,ymax,xmax])
Résultat Perspective

Résultat
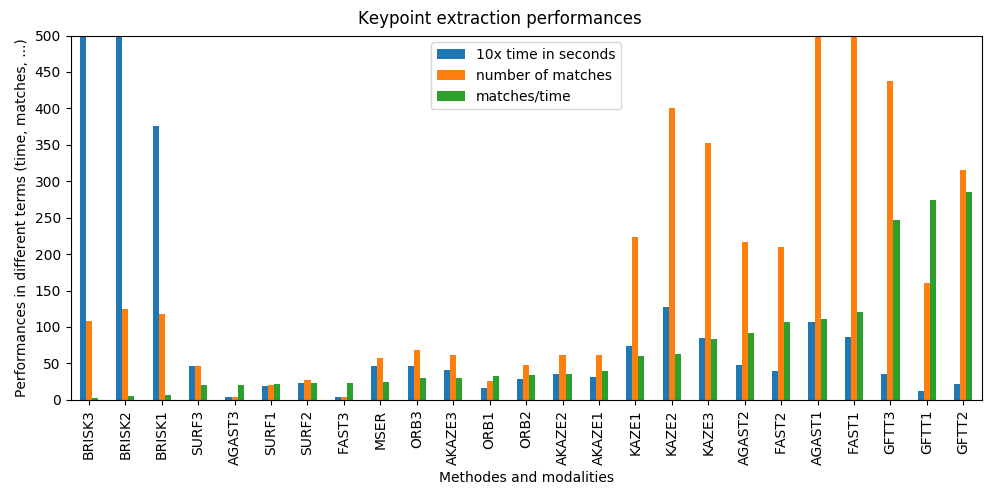
Comme dit plus haut, tout les algorithmes de points-clé ont été évaluer ainsi que toutes les bandes spectrales de référence. Seul ces paramètres changes dans l'algorithmes, ce qui permet de les comparer facilement. Donc toutes ces méthodes fonctionnent (globalement), le choix de la méthode dépend de l'équilibre entre temps de calcul et précision que l'on souhaite :
- Les GFTT affichent les meilleures performances par rapport à toutes les autres, tant en termes de temps de calcul que de nombre de correspondances trouvées
- FAST et AGAST est sont appropriés, équilibrés entre temps et performances et nombre de correspondances trouvées.
- KAZE montre un bon nombre de matchs (>200) mais il est aussi 2,5 fois plus lent que FAST/AGAST.
Les autres n'ont pas montré d'amélioration en termes de performances ou de matchs :
- AKAZE et MSER n'ont pas montré d'avantages par rapport à FAST.
- SURF peut convenir, mais ne montre pas d'avantages par rapport à FAST.
- ORB peu être exclu, le nombre de correspondances est proche de ~20 minimum pour s'assurer que l'homographie est correcte.
- BRISK montre un bon nombre de correspondances, mais le temps de calcul est trop long (~79 sec) par rapport à FAST (~8 sec).
L'augmentation du nombre de points clés appariés montre une plus grand précision. Par exemple, passer de SURF (~30 correspondances) à FAST (~130 correspondances) montrent des distances résiduelles finales réduites de ~1,2px à ~0,9px et le temps de calcul de ~5sec à ~8sec. Toutes les méthodes montrent que le meilleur spectre de référence est de 710 nm, exécuté pour SURF et GFTT qui est 570 nm. La figure suivante montre le nombre minimum de correspondances entre chaque spectre de référence et tous les autres en utilisant l'algorithme FAST.
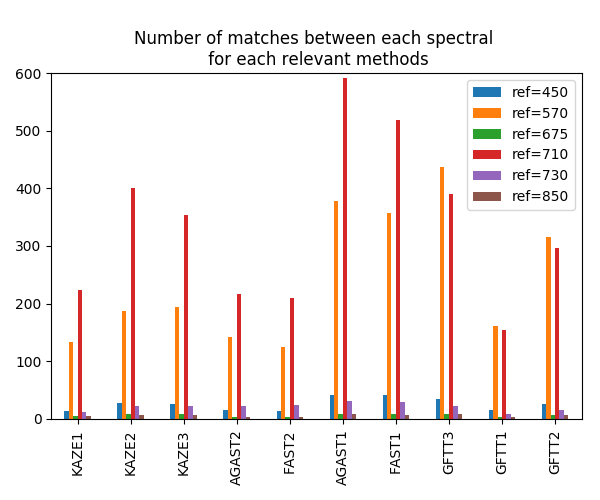
Une fois que les meilleurs extracteurs de points clés et la meilleure référence spectrale sont définis, nous utilisons leur détection pour estimer une homographie. L'homographie est un isomorphisme des perspectives. Une homographie 2D entre A et B nous donne la transformation de projection entre les deux images. C'est une matrice 3x3 qui décrit la transformation affine.
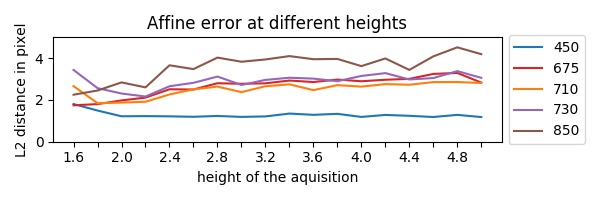
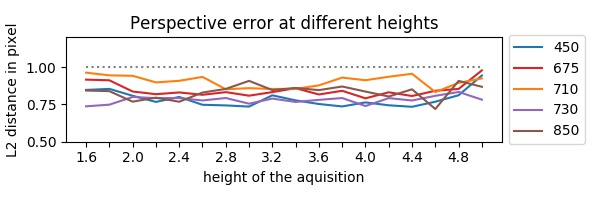
Les résidus de la correction de perspective montrent que nous avons correctement enregistré chaque bande spectrale, la figure (en bas) indique la distance résiduelle à différentes distances au sol. En comparaison, l'erreur de correction affine est comprise entre $[1,0-4,8] px$ où la combinaison de la correction affine et de la correction en perspective ; l'erreur résiduelle est comprise entre $[0,7-1,0] px$. En moyenne, la correction en perspective augmente l'erreur résiduelle de $(3,5-0,9)/3,5$ environ 74%.
Conclusion
Dans ce travail, on a exploré l'application de différentes techniques pour l'enregistrement d'images multispectrales. Nous avons testé différentes méthodes d'extraction de points clés à différentes hauteurs et le nombre de points de mise en correspondances obtenus. Comme on l'a vu sur la méthode, la méthode la mieux adaptée est la méthode GFTT avec un nombre minimum de correspondances et un temps de calcul "raisonnable". De plus, la meilleure référence spectrale a été définie pour chaque méthode, comme 710 pour GFTT. Nous observons une erreur résiduelle inférieure à $1 px$.