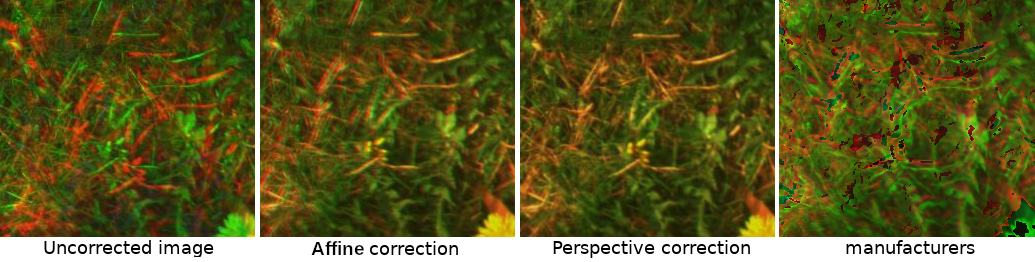
Résultat

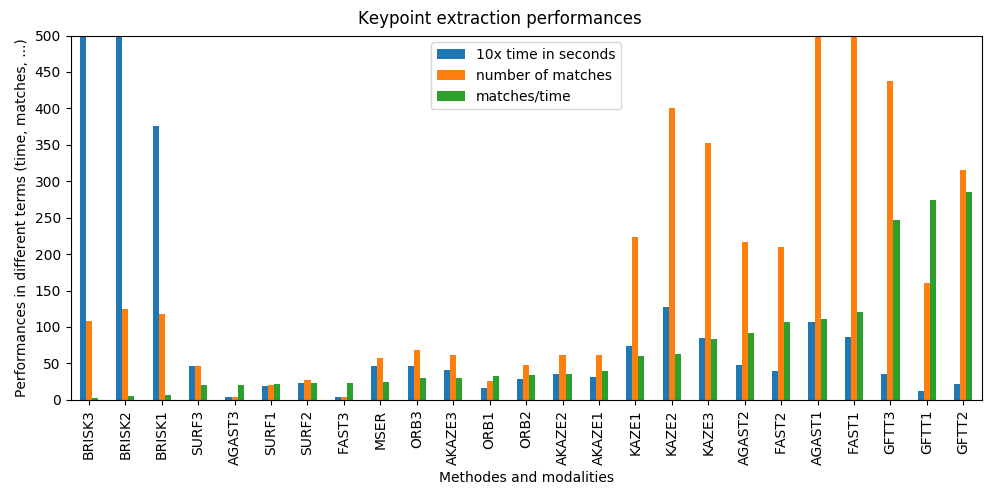
Comme dit plus haut, tout les algorithmes de points-clé ont été évaluer ainsi que toutes les bandes spectrales de référence. Seul ces paramètres changes dans l'algorithmes, ce qui permet de les comparer facilement. Donc toutes ces méthodes fonctionnent (globalement), le choix de la méthode dépend de l'équilibre entre temps de calcul et précision que l'on souhaite :

• Les GFTT affichent les meilleures performances par rapport à toutes les autres, tant en termes de temps de calcul que de nombre de correspondances trouvées
• FAST et AGAST est sont appropriés, équilibrés entre temps et performances et nombre de correspondances trouvées.
• KAZE montre un bon nombre de matchs (>200) mais il est aussi 2,5 fois plus lent que FAST/AGAST.

Les autres n'ont pas montré d'amélioration en termes de performances ou de matchs :

• AKAZE et MSER n'ont pas montré d'avantages par rapport à FAST.
• SURF peut convenir, mais ne montre pas d'avantages par rapport à FAST.
• ORB peu être exclu, le nombre de correspondances est proche de ~20 minimum pour s'assurer que l'homographie est correcte.
• BRISK montre un bon nombre de correspondances, mais le temps de calcul est trop long (~79 sec) par rapport à FAST (~8 sec).

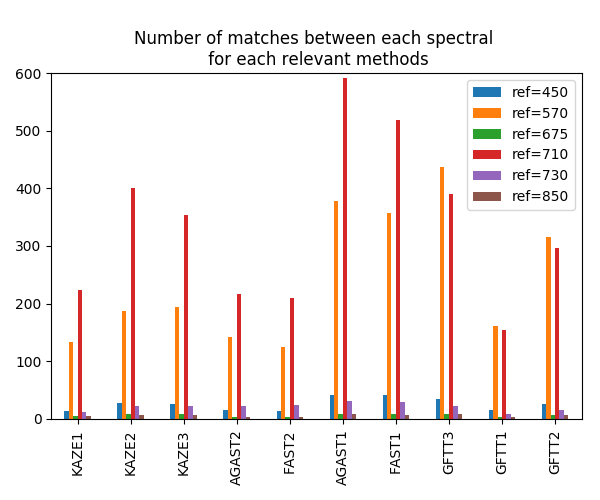
L'augmentation du nombre de points clés appariés montre une plus grand précision. Par exemple, passer de SURF (~30 correspondances) à FAST (~130 correspondances) montrent des distances résiduelles finales réduites de ~1,2px à ~0,9px et le temps de calcul de ~5sec à ~8sec. Toutes les méthodes montrent que le meilleur spectre de référence est de 710 nm, exécuté pour SURF et GFTT qui est 570 nm. La figure suivante montre le nombre minimum de correspondances entre chaque spectre de référence et tous les autres en utilisant l'algorithme FAST.

Une fois que les meilleurs extracteurs de points clés et la meilleure référence spectrale sont définis, nous utilisons leur détection pour estimer une homographie. L'homographie est un isomorphisme des perspectives. Une homographie 2D entre A et B nous donne la transformation de projection entre les deux images. C'est une matrice 3x3 qui décrit la transformation affine.

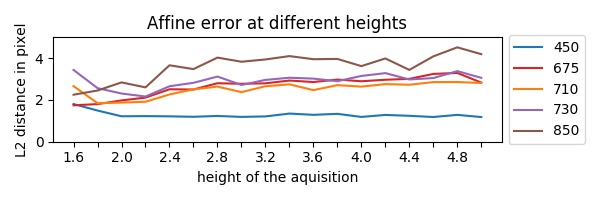
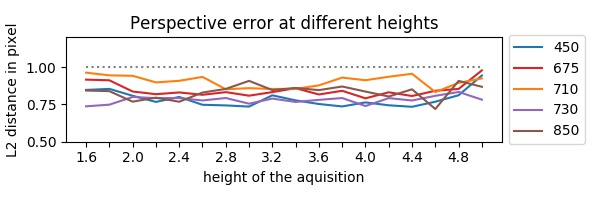
Les résidus de la correction de perspective montrent que nous avons correctement enregistré chaque bande spectrale, la figure (en bas) indique la distance résiduelle à différentes distances au sol. En comparaison, l'erreur de correction affine est comprise entre $[1,0-4,8] px$ où la combinaison de la correction affine et de la correction en perspective ; l'erreur résiduelle est comprise entre $[0,7-1,0]  px$. En moyenne, la correction en perspective augmente l'erreur résiduelle de $(3,5-0,9)/3,5$ environ 74%.

Conclusion

Dans ce travail, on a exploré l'application de différentes techniques pour l'enregistrement d'images multispectrales. Nous avons testé différentes méthodes d'extraction de points clés à différentes hauteurs et le nombre de points de mise en correspondances obtenus. Comme on l'a vu sur la méthode, la méthode la mieux adaptée est la méthode GFTT avec un nombre minimum de correspondances et un temps de calcul "raisonnable". De plus, la meilleure référence spectrale a été définie pour chaque méthode, comme 710 pour GFTT. Nous observons une erreur résiduelle inférieure à $1 px$.