Introduction à la classification statistique
Les techniques se basant sur les lois statistiques sont les premières qui ont été utilisées pour l’analyse de données. Elles consistent à prendre un sous ensemble d’une population et essayer d’arriver à des conclusions concernant toute la population. Ce sont des méthodes qui reposent sur la théorie de Bayes représentant une référence théorique pour les approches statistiques de résolution des problèmes de classification.
Ici le but est de retrouver la distribution d’une ou plusieurs classe afin de prévoir l’information à partir d’une fonction de densité de probabilité connue et donc plus facile à travailler, pour ce TP nous nous limiterons à une équations loi normale/gaussienne. Nous allons de plus utiliser une approche Bayésienne. C’est une méthode d’estimation à posteriori d’appartenance à une classe K en fonction de sont équation de densité de probabilité afin de minimise la probabilité d’erreur de classement, avec ∫(densité)=1.
Lorsqu’il y a recouvrement par deux classe différentes pour un seul item à estimer, c’est la classe dont la probabilité la plus forte qui prend donc l’avantage. Mais, lorsque les classes ont la même probabilité, comme dans le diagramme ci-dessus, l’approche Bayésienne est insuffisamment, et l’on peut donc « augmenter » l’analyse par paramétrisation (probabilité différentes par classe) ou en ajoutant d’autres descripteurs pour les données étudier.

En résumé, la règle de décision de Bayes constitue la limite optimale de tout système de classification. Malheureusement cette limite est théorique : en effet, face à un problème réel, les distributions des classes sont inconnues, ainsi que les probabilités a posteriori. Les différentes méthodes mathématiques de résolution peuvent seulement en fournir des estimations. Cette erreur théorique constitue une borne infranchissable qui représente d'une certaine manière la difficulté intrinsèque du problème.
1°) L’analyse des données
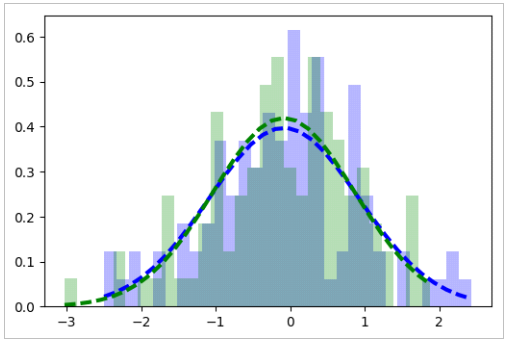
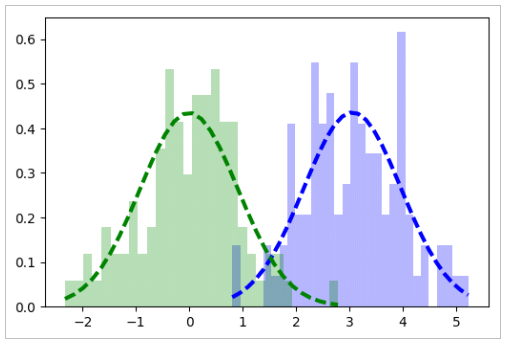
On dispose de 3 classes de points en dimenssion 2, on obtient donc 6 histogrammes différents : une pour chaque dimensions, puisque les données x et y ne sont pas forcement liée (nôtres cas). Pour visualisées cela, modifier la fonction « affichage_histogramme_loinormale » pour pouvoir interpréter correctement les résultat visuellement, par superposition :
L’histogramme violet correspond à la composante X, l’histogramme jaune correspond à la composante Y et les lois normales sont de la même couleur que les composantes. Nous pouvons donc conclure que, dans ces exemples, les composantes des classes 1, 2 et 3 suivent une distribution selon une loi Normale (ou Gaussienne). Pour extraire les centroides et les matrices de covariance nous pouvons définir une fonction :
def apprentissage_loi_normale(liste_donnees_classe): tab_donnees = array(liste_donnees_classe) vect_moyenne = mean(tab_donnees, axis = 0) mat_covariance = array(cov(tab_donnees.transpose())) return [vect_moyenne, mat_covariance]
Les centroïdes et matrices de covariances associées ont été extraits grâce à cette dernière :
| classe | centroïdes | Matrice de covariance |
|
1 |
[-0.08334193 -0.08541702] | [ 1.0175364, -0.07091903] [-0.07091903, 0.91352591] |
|
2 |
[2.93982437 3.08713358] | [ 1.18931151, -0.03957458] [-0.03957458, 1.16833718] |
|
3 |
[ 3.05691106 -0.00513458] | [ 0.8475625, 0.11541681] [ 0.11541681, 0.85057838] |
À priori les composantes sembles indépendantes (les éléments non diagonaux sont proches de zero)
2°) Apprentissage des paramètres de la loi normal
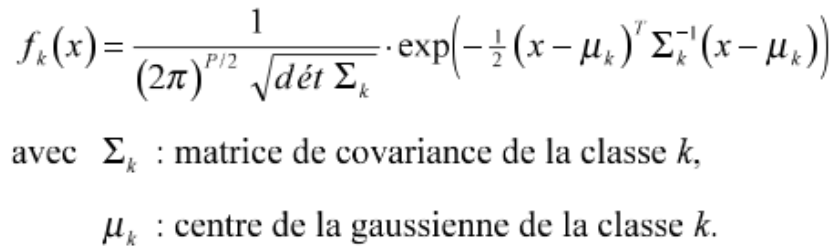
La figure précédente présent l'équation d'une loi normal. Nous pouvons constater que le premier terme reste contant et nous pouvons enlever l’exponentiel en passant tous les calcules en log. Finalement ont prend le maximum de cette évaluation sur toutes les classes qui nous donne l’estimation avec une équiprobabilité entre les classes pour l’élément. Ce qui ce traduit par l’embryon de code suivant :
def calcul_vraisemblance_loi_normale(donnee,liste_parametres,diago,proba): result = [0] * len(liste_parametres) tab = (liste_parametres) data = array(donnee) for i in range(0,len(liste_parametres)): vecti = array(tab[i][0]) covi = array(tab[i][1]) xmoinsui = donnee - vecti deti = -0.5*log(det(covi)) result[i] = deti + -0.5*dot(xmoinsui,inv(covi)) return [argmax(result),result]
3°) Classification : Décision par maximum de vraisemblance
Cette algorithme à donc été appliqué sur nos données et les résultats souhaité sont correctement estimer, mais puisque le terme -1/2 à été garder pour correspondre au équation vue, avec l’utilisation de argmax, les données de vraisemblances sont négatives :
La donnee de classe 1 a ete reconnue comme une donnee de classe 1
Vraisemblances : [-1.009520059808324, -21.06057881454943, -10.813993119251792]
La donnee de classe 2 a ete reconnue comme une donnee de classe 2
Vraisemblances : [-39.339460248628669, -3.076525403568477, -27.638713611242224]
La donnee de classe 3 a ete reconnue comme une donnee de classe 3
Vraisemblances : [-11.380127875408361, -6.0101523104161858, -0.18302033798559841]
4°) Probabilité à priori
Les calcules effectué précédemment reste vrai, il suffi d’introduire le terme correspondant à la probabilité de la classe, qui correspond à « log(proba[i]) ». Le choix d’utilisation du paramètre des probabilitées des classes est données :
if proba != None : res = res + log(proba[i])
test:
| Proba | [0,1,0] | [998.0/100, 1/100, 1/100] |
| Classe reconnu | 2, 2, 2 | 1, 2, 1 |
5°) Optimisation
L’optimisation proposé repose sur les propriétés des matrices diagonales (donc carrées). En effets l’inversion d’une matrice diagonal peut-être largement simplifier. Si le déterminant de la matrice diagonal est non-nul, dans ce cas, l’inversion correspond au inverse des coefficients diagonaux de la matrice de départ. Et le déterminant d’une matrice diagonal est simplement le produit des coefficients diagonaux : ∏M[i,i]
Dans notre cas, c’est une matrice de covariance, dont les élément diagonaux sont les variances des classes. Ces variance sont rarement nul (aucune dispersion) puisque d’une probabilité impossible dans le monde réel. De plus, si les éléments non diagonaux (les covariances) sont toutes proches de zéro, alors nous pouvons supposé qu’il n’y a pas de dépendance entres les données et peuvent alors être « ignorer ». Donc par hypothèse la matrice est diagonal, et inversible.
Nous pouvons aussi éliminer la multiplication de la matrice et la section de code concerné à donc été modifier comme suit :
# diago est une variable pour forcé l’hypothèse que covi est diagonal if diago == True : covi = diag(covi) # le vecteur de la diagonal deti = prod(covi) # le produit des coéficients diagonaux deti = -0.5*log(deti) for i in range(0,len(xmoinsui)): # minus car facteur de -1/2 et propriété du logarithme sur division final_right_terme = final_right_terme - pow(xmoinsui[i],2)/covi[i] else: deti = -0.5*log(det(covi)) #membre gauche invi = inv(covi) right_terme = -0.5*dot(xmoinsui,invi) final_right_terme = dot(right_terme,xmoinsui)
Les données reste correctement estimer ! Cependant nous pouvons constater que lors de l’utilisation de classe non-équiprobable l’approximation de l’erreur engendre un calcule faux de l’estimation (division par zéro)
6°) Exemple

Encore une fois le module sklearn prose différentes approche basé sur Bayes.
from sklearn.mixture import GaussianMixture from sklearn.naive_bayes import GaussianNB