Petite Introduction a l’algorithme du perceptron
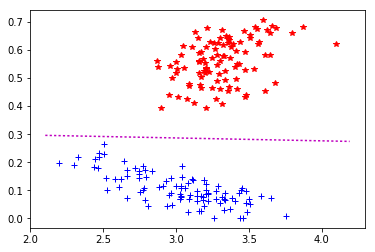
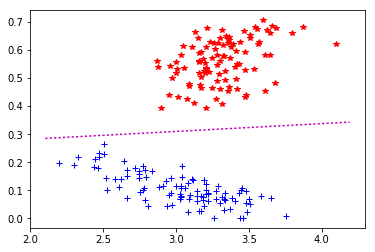
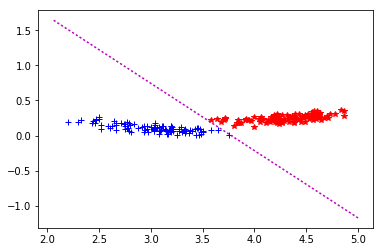
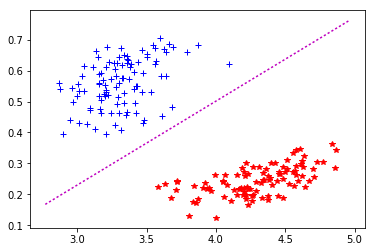
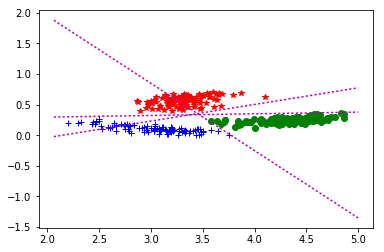
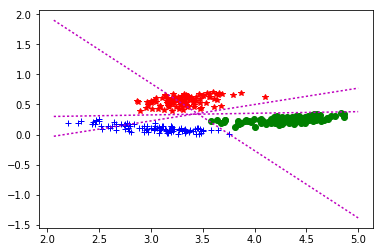
Le perceptron est un modèle de réseau de neurones avec algorithme d'apprentissage créé par Frank Rosenblatt en 1958. Nous alons étudier ici, l’algorithme du perceptron (batch), cette algorithme aide à trouver une droite de séparation entre deux set de données par descente de gradiant afin détablir une classification des données entrées. Le perceptron recherche donc l'hyperplan séparateur entre les deux classes de points, avec mu qui represente la vitesse de descente. Il renvoi la liste w (w0, w1, w2) des coefficients de l'équation de l'hyperplan séparateur.
Implémentation:
def accumulate(data, delta): acc = np.zeros(17) for point in data: # ajout terme d'erreur au point : point = [x, y, 1.] p = np.array([*point, 1.0]) # calcul du produit scalaire entre le point et w prod = vdot(p,w) # accumulation de delta * p pour les points mal classés if (prod*delta <= 0): acc -= delta*p return acc
def perceptron(dataGroupe1,dataGroupe2,mu,maxit=1000): # initialisation quelconque de w w = np.zeros(17) w[15] = -1.0 w[16] = 1.0 for i in range(maxit): # classe 1 : classe positive (point.w > 0) donc on prend delta= 1. acc = accumulate(dataGroupe1, 1) # classe 2 : classe négative (point.w < 0) donc on prend delta=-1. acc += accumulate(dataGroupe2, -1) # mise à jours des paramètres de l'hyperplan (descente de gradient) w = w - (mu/i)*acc # s'il n'y a pas suffisement d'amélioration alors c'est un minimum local # on peu donc conclure à une stabilisation de l'algorithme et le terminer regulation = np.sqrt(np.sum(wold**2)) if np.linalg.norm(w,wold,2) / regulation < 0.001: return w return w
Les testes effectuer :
Les jeux de données présenté ne permettent pas de tester tous les cas de figures, surtout quand on souhaite utiliser l’algorithme sur 3 jeux de données simultanément : pas de « triangle » recouvert par plusieurs sets. On noteras de plus qu'initialisé mu avec une très grande valeurs ne permet pas de converger. Nous pouvons également généralisé l'approche à plusieurs classes en définissant des droites de séparation pour chaque couple de classe.
Conclusion :
Au final après plusieurs testes effectuer sur les jeux proposé, mu ne semble pas beaucoup influer la droite quand il est dans [1,0 et 999,0] et retourne un résultat intéressant avec un nombre d’itération qui ne varie pas beaucoup. Par contre si mu est fixer dans ]0,0 et 1,0[ ont augment largement le nombre d’itération mais égalements l’erreur d’estimation de l’équation de la droite de séparation des deux classes.
| mu | 1 | 10 | 100 | 1000 | 10000 |
| iteration | 8 / 15 / 24 | 8 / 15 / 24 | 8 / 15 / 25 | 8 / 15 / 25 | 8 / 15 / 25 |
| mu | 0.75 | 0.5 | 0.1 | 0.05 | 0.01 |
| iteration | 8 / 15 / 32 | 8 / 16 / 32 | 23 / 16 / 28 | 8 / 19 / 36 | 9 / 57 / 249 |
L’analyse serait plus difficile si les deux nuages de point avais une zone de recouvrement conjointe, et c’est la que la configuration de mu permet à l’algorithme d’être plus « précis » sachant que de meilleurs algorithme existe dans ces situations la. (que nous allons peut-être voire plus tard).

source : données issue de http://mlpy.sourceforge.net
Le module sklearn propose bien entendue ce type d'analyse :
from sklearn.datasets import load_digits from sklearn.linear_model import Perceptron clf = Perceptron(tol=1e-3, random_state=0) clf.fit(X, y)