Objectif et présentation

L'algorithme des kppv (k plus proche voisin) ou knn (k nearest neighbor) est un algorithme de classification et de regression. La méthode des K-plus proches voisins consiste à affecter, à un point à classer, la classe majoritaire de ses K plus proches voisins. L'algorithme est plutot simple et est très semblable à l'algorithme des kmeans précédement illustré. On pré-calcule la distance entre le point à classer et l’ensemble des autres points de toutes les classes en ce rappelant d’où viens le point (index de la classe et l’index dans la classe) et on prend les k premiers. 

 Nous allons donc implémenter cette algorithme !

def decision_kppv(data,point_a_classer,K,heuristique):
    nb_classes = len(data)
    nb_points_representatifs = len(data[0])

Implémentation

Pour ce faire, on va simplement utiliser un buffer pour chaque classe avec comme information un vecteur composé de la distance et du point dans la classe, une fois l’ensemble calculé, ont range chaque buffer par distance :

distance=[]
for i in range(0,nb_classes):
    distance.append([]);
    for j in range(0,len(data[i])):
        distance[i].append([np.linalg.norm(data[i][j], point_a_classer),data[i][j]])
    # ont trie par distance au point
    distance[i] = sorted(distance[i], key=lambda x: x[0])
    # finalement ont prend les K plus proche
    distance[i] = distance[i][0:K]

Ensuite, ont refait le même type d’opération mais, cette fois ci, les données sont déjà classées, donc on va pouvoir prendre les k plus petites distances parmi les nb_classes des buffers précédemment décris

all_dist = [0]*nb_classes;
all_point = [0]*nb_classes;
for j in range(0,nb_classes):
    all_dist[j] = distance[j][0][0]
    all_point[j] = distance[j][0][1]
all_min = min(all_dist);
all_index = all_dist.index(all_min)

On stocke le résultat dans deux nouveaux buffers, qui contiendront respectivement les distances et les indices des classes d’origine. Nous avons donc les distances et les classes associées.

distance[all_index].pop(0)
Kdisplay.append(all_point[all_index])
god_distance.append(all_min)
god_classes.append(all_index)

Il nous reste à déterminer à quelle classe le point à classer appartient, puisque nous avons les indices des classes associées il nous suffit de compter le nombre d’occurrence de chaque classe et de prendre la classe qui a le plus de représentants.

counts = []
for i in range(0,nb_classes):
    counts.append(god_classes.count(i))
counts_max = max(counts)

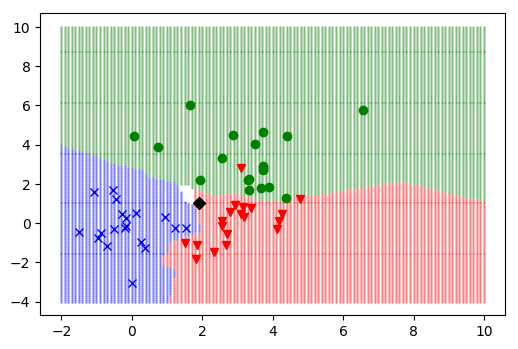
Par exemple sur la figure suivante, pour classer le point noire [1.9, 1.025], on cherche les K=8 plus proche voisin, et les classes trouvées sont [2, 2, 2, 1, 0, 2, 0, 2] puis ont les comptes (rose=1, jaune=2, turquoise=5), le point seras donc classé dans la classe rouge.

La donnee de classe 1 a ete reconnue comme une donnee de classe 1
La donnee de classe 2 a ete reconnue comme une donnee de classe 2
La donnee de classe 3 a ete reconnue comme une donnee de classe 3

Traitement du cas d’égalité

Si le nombre maximum d’occurrence dans le dernier tableau calculé apparaît plusieurs fois, il y a donc une ambiguïté, par exemple avec k=8, si on trouve [3, 2, 3] alors la classe 1 et la classe 3 sont toutes deux solutions des k-ppv. Dans ce cas il y a plusieurs approches possible :

• on prend la classe du point le plus proche → inutile
• on prend la classe du point moyen de la classe la plus proche
• on incrémente K ou on décrémente K (au pire K=1 et on trouve forcément → premier cas), sinon on converge forcément vers une solution
• on ajoute une probabilité pour chaque classe utilisée pour multiplier le vecteur du nombre des classes représentées ex : [3, 2, 3] * proba
  si on prend des valeurs différentes mais proches on est sur d’avoir un maximum locale unique
• on utilise un meilleur algorithme, on peux faire mieux avec un kd-tree

Ces différentes heurisitques peuvent être implémentées :

total = counts.count(counts_max) 

if heuristique == "average" and total > 1:
    all_min = [0]*nb_classes
    all_min_count = [0]*nb_classes
    for i in range(0, nb_classes):
        for j in range(0, K):
            if god_classes[i] == j and counts[i] == counts_max:
                all_min[i] += god_distance[j]
                all_min_count[i] += 1
        if all_min_count[i] != 0:
            all_min[i] /= all_min_count[i]
        else:
            all_min[i] = +inf
    minimum = min(all_min)
    classe_la_plus_proche = all_min.index(minimum)+1
        
elif total > 1 and heuristique == "random":
    classe_la_plus_proche = 0
    classe_random = randint(1,total)
    while classe_random>1:
        counts[counts.index(counts_max)] = -inf
        classe_random = classe_random-1
    classe_la_plus_proche = counts.index(counts_max)+1

elif total > 1 and heuristique == "incrementk":
    return decision_kppv(data,point_a_classer,K+1,"incrementk")

elif total > 1 and heuristique == "decrementk":
    return decision_kppv(data,point_a_classer,K-1,"decrementk")

elif total > 1 and heuristique == None:
    # inclassable -> classe 0
    return 0

else:
    #print("yolo",point_a_classer,"-->",counts.index(counts_max)+1)
    classe_la_plus_proche = counts.index(counts_max)+1

Choix des paramètres

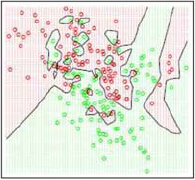
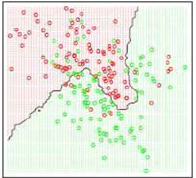
Comment bien choisir K (le nombre de voisin à prendre en considération) ? Si K est trop petit la classification est trop sensible au bruit (image de gauche K=1). À l'inverse si K est trop grand, la classification peut-être erroné par une trop grande zone de décision (image de droite K=15).

Le choix de K est donc dépendant des données en entrée :

• s’il y a une grande dispersion (grand écart-type) → K « grand »
• si les données sont entrelacées et que le point à classer est dans le nuage → K « moyen »
• si le point à classer est en dehors des nuages on peut choisir → K « petit »
• on peut optimiser cette approche avec un kd-tree pour connaître la configuration locale
• dans tous les cas, nb_classes ≤ K ≤ sqrt(nb_point)

Faut-il prendre un nombre de point représentatifs élevés comme ensemble d’apprentissage ?

• Si on prend un très grand nombre de points représentatifs :
  • l’apprentissage est plus précis et minimise les erreurs de classification
  • par contre il est aussi beaucoup plus lent → donc non
• Si on prend un trop faible nombre de points représentatifs :
  • l’apprentissage est erroné et l’ajoute d’heuristique est nécessaire
  • par contre l’apprentissage est très rapide
• Cette fois ci le choix du nombre de représentants est dépendant du point à classer et du nombres de classes.

Qu’est ce qui va vous guider pour arriver à obtenir un choix idéal sur ces deux paramètres ?

Comme dit plus haut il n’y a pas de « bonne méthode » pour le choix des paramètres, comme les deux paramètres sont dépendants de critères différents, le seul choix possible c’est de laisser un humain expérimenter plusieurs solutions pour minimiser l’erreur de classement. Pour bien faire il faudrait s’intéresser à la théorie des statistiques, des thèses sont disponibles, mais l’algorithme lui même est limité, il faut nécessairement chercher d’autres approches pour trouver de meilleurs résultats de classement sans intervention humaine (choix des paramètres et des heuristiques). Dans certain cas lorsque le domaine étudié est connu on peux construire une base de données et « augmenter » les critères de choix, ce qui n’est pas applicable ici.

Par exemple, comment classer un point au centre de ce nuage ? Avec quels paramètres ? Il n’y a pas de bonne réponse, il vaux mieux un algorithme qui dit clairement que le point n’est pas classable. On sait au moins qu’il ne faut pas choisir K pair ce qui augmente les probabilités d’indécision sur les bordures des classes. Autrement il faut tester les différentes valeurs de K sur nos données :

Frontière de décision

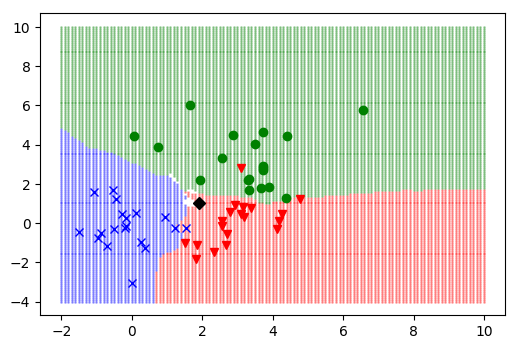
Pour afficher la frontière de décision on peut calculer pour « tous » les points de l’espace la décision prise par k-ppv ce qui nous génère une carte :

Si on veux aller plus loin il suffit de détecter les contours des points lorsqu’il y a d’autres points de couleurs différentes, par contre on commence à voir les limites de performances de python …

Annexe

Pour finir voici quelques exemple avec différentes valeur de K et différentes heuristique pour K=4 :