Coloration d'un graphe

Définition 1 : Soit $G=(X,U)$ un graphe non-orienté. Un sous ensemble $S \in X$ est un ensemble stable s'il ne comprend que deux sommets non-adjacents deux-à-deux $\forall x_i, x_j \in S \implies (x_i, x_j) \not\in U$ Comme tout sous-ensemble stable est aussi un ensemble stable, il convient de chercher le cardinal maximum d'un ensemble stable. Ce nombre est noté $\alpha(G)$ et est appelé le nombre de stabilité.

Définition 2 : Colorier un graphe c'est colorier les sommets de telle sorte que deux sommets distincts et adjacents aient toujours des couleurs différentes. Le nombre chromatique est le plus petit nombre de couleurs nécessaires pour colorier le graphe. Le nombre chromatique $\phi(G)$ est définit comme le nombre minimal de couleurs nécessaires à la coloration de G. Un graphe G tel que $\phi(G) <= k$ qui est coloriable en k couleurs est dit k-chromatique.

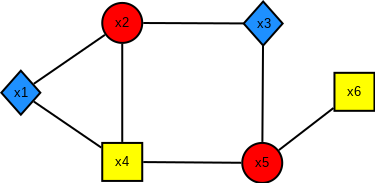
Exemple 1 : $S_1 = \{x_1, x_2, x6\} ; S_2 = \{x_2, x_5\}, S_3 = \{x_4\}$

Borne inférieur du nombre chromatique : Puisque \alpha(G) est le nombre maximum des sommets des ensembles stables déduits de G, on a $\alpha(G) \times \phi(G) >= n(G) \implies \phi(G) >= \frac{n(G)}{\alpha(G)}$. Dans notre exemple précédent $\alpha(G) = \max(Card(S_1), Card(S_2), Card(S_3)) = \max(3,2,1) = 3$ et donc $\phi(G) >= \frac{6}{3} => 2$.

Borne supérieur du nombre chromatique : Une borne supérieur est donnée par $deg+1$, avec $deg$ le plus grand degré d'un sommet. Dans l'exemple précédent $deg=3$.

Encadrement du nombre chromatique : En utilisant les deux notions précédentes, le nombre chromatique peu être borné par $\frac{n(G)}{\alpha(G)} <= \phi(G) <= deg+1$. Soit $2 <= \phi(G) <= 4$ dans l'exemple précédent.

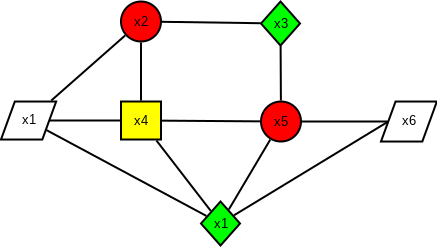
Exemple 2 : $n(G) = 7 ; S1=\{x1, x_6\} ; S_2=\{x_2, x_5\} ; S_3=\{x_3, x_7\} ; S_4 = \{x_4\}$

Dans cette exemple 2, en réutilisant les formules précédentes, nous donnons $\alpha(G) = 2$ qui nous permet d'obtenir le nombre chromatique $\phi(G) = \frac{7}{3} >= 3$. Le degré du graphe est de $4$, ce qui nous donne l'encadrement chromatique $\frac{7}{3} <= 3 <= 4+1$.

Algorithme de coloriage des sommets d'un graphe simple

bla bla ...

1. On range les sommets dans un tableau en ordre de degré décroissant
2. On attribue la couleur $C_1$ à $X_1$ et au premier sommet de la liste qui n'est pas adjacent à $x_1$
   et ainsi de suite avec les sommets de la liste qui ne sont pas adjacents aux sommets déjà coloriés
3. On attribue la couleur $C_2$ au premier sommet non colorié
   ainsi qu'aux sommets suivants qui ne sont pas adjacents aux sommets coloriés par la couleur $C_2$
4. On répète ce processus jusqu’à épuisement des sommets de la liste

Basé sur l'exemple 2, l'algorithme donne le tableau suivant :

Implémentation en python

bla bla

Application en cartographie

bla bla