Correction des couleurs

L'objectif de la correction des couleurs est de modifier les valeurs de chaque canal chromatique sur l’ensemble des pixels d’une image de telle sorte que les valeurs mesurées après la transformation soient le plus proches possible de celles mesurée avant la numérisation. Plusieurs fonctions ont été testées pour rectifier l’altération des couleurs. L’ensemble des modèles construits pour restaurer la constance des couleurs ont été calibrés à partir des modalités chromatiques référencées d’une part dans une matrice après numérisation et, d’autre part, à partir des modalités chromatiques enregistrées dans une matrice avant la numérisation. L'article de D. Varghese en montre l'utilisation. Exemple d'aberation colorimetriques sur des chevres :

Chaque algorithme a été ajusté à l'aide d'un vérificateur de couleur "x-rite classique". Le vérificateur de couleurs est une grille imprimée de 24 carrés colorés, où chaque couleur est normalisée, référencée et optimisée pour la correction des couleurs. Nous avons pris une photo du vérificateur de couleurs avec un fond noir, et nous avons extrait la couleur en utilisant la vision par ordinateur. Pour chaque carré détecté nous calculons la couleur moyenne pour éliminer le bruit. Le modèle de correction des couleurs a été vérifié avec l'équation de la distance de couleur perçue deltla cie 2000 presenter plus bas, entre la matrice des couleurs rectifiées et celle des couleurs attendues.

Une couleur peut être représentée dans un espace chromatique par trois points, dont les coordonnées correspondent aux valeurs des trois couleurs primaires rouge, vert et bleu. Lors de la numérisation, l’instabilité de l'éclairage et la sensibilité des capteurs numériques modifient la position de ces points et entraîne un changement dans la perception des couleur. Biensur d'autres espace colorimetrique sont possibles.

points : turquoise = destination ; jaune = perturbé ; rose = corriger

Et a partir de ces premiers informations nous pouvons tester differents modeles de corrections presente ci-dessous :

Transformation rigide

Nous essayons de faire correspondre une "transformation de corps rigide" 3D à des ensembles de points 3D (couleurs) donnés "depuis" $y_i$ (perturbé) et "vers" $x_i$ (corrigé). Plus précisément, nous recherchons une rotation, une échelle et une translation qui minimise la somme des carrés des "erreurs" $E = \sum_{i=1}^{n}||\mathcal{R} x_i + t_{x,y} - y_i|||^2$. Ainsi, la transformation $\mathcal{R} + t_{x,y}$ peut s'écrire sous la forme d'une matrice homogène $3 \times 3$, paramétrée par $\alpha, \beta, \lambda$ et le vecteur de traduction $t_{x,y}$. Où $\alpha$ sont l'angle «lacet», $\beta$ l'angle «tangage», $\lambda$ l'angle «roulis». L'estimation couramment utilisée de $\mathcal{R}$ et de $t_{x,y}$ recentre chaque points du nuage denote $\overline{x_i}$ et $\overline{y_i}$. La différence de centroïde ($\overline{y_i}-\overline{x_i}$) correspond au vecteur de translation $t_{x,y}$. Pour estimer le $\mathcal{R}$, nous utilisons une décomposition en valeur singulière de la matrice $\overline{x_i}^T \overline{y_i}$, R est réflexif lorsque le $\det \mathcal{R}$ est négatif.

def rigid_transform(A, B):
    assert len(A) == len(B)
    N = A.shape[0];

    centroid_A = np.mean(A, axis=0)
    centroid_B = np.mean(B, axis=0)
    AA = A - np.tile(centroid_A, (N, 1))
    BB = B - np.tile(centroid_B, (N, 1))

    H = np.transpose(AA) * BB
    U, S, Vt = np.linalg.svd(H)
    R = Vt.T * U.T

    # special reflection case
    if np.linalg.det(R) < 0:
       Vt[2,:] *= -1
       R = Vt.T * U.T

    t = -R*centroid_A.T + centroid_B.T
    return R, t

Régression polynomiale

La régression polynomiale consiste à améliorer la proximité de notre modèle par rapport aux données en augmentant l'ordre des relations entre les facteurs et les variables de réponse. Differents ordres de l'équation linéaire $p(y_i) = a_n y_i^n + a_{n-1} y_i^{n-1} + ... a_2 y_i^2 + a_1 y_i + a_0$ a été testé (où $a_0$ est la correction du point blanc). La déclaration selon laquelle $p$ interpole les points de données signifie que $x_i = p(y_i)$. L'expression polynomiale précédente peut être écrite sous la forme d'un système d'équation linéaire sous la forme $Ax=b$. Une fois de plus, le système linéaire est approximé en utilisant une décomposition en valeurs singulières. La solution minimise l'erreur au carré $E = \sum_{j=0}^k |p(x_j) - y_j|^2$ dans le système précédent ($Ax=b$). Il s'agit d'un cas particulier de régression linéaire multivariée.

def nd_order_colour_fit(target, detected, order=3):
    pr = np.poly1d(np.polyfit(detected[:,2], target[:,2], order))
    pg = np.poly1d(np.polyfit(detected[:,1], target[:,1], order))
    pb = np.poly1d(np.polyfit(detected[:,0], target[:,0], order))
    return (pb, pg, pr)

Regression lineaire multivariée

Nous nous intéressons à l'impact non seulement d'un, mais de nombreux facteurs différents sur la variable de réponse. Cette variable est généralement plus représentative des problèmes du monde réel que le modèle de stock à facteur unique par rapport à la réponse décrit ci-dessus (régression polynomiale). L'équation qui décrit régression linéaire multivariée pourrait s'écrire comme suit : $x_i = p(y_i) = a_3 r + a_2 g + a_1 b + a_0$ où $a_i$ et sont les coefficients des facteurs $x_i$ et $x_0$ est la correction du point blanc.

def first_order_colour_fit(m_1, m_2):
    system = np.linalg.lstsq(m_1.reshape(24,3), m_2.reshape(24,3))
    foc = np.transpose(system[0])
    foc = np.matrix(foc)
    return foc

Regression polynomial multivariée

En outre, nous proposons d'utiliser la régression polynomiale. Elle calcule la relation entre une variable dépendante avec une ou plusieurs variables indépendantes (prédicteurs), et ces variables indépendantes. Par exemple, pour une variable indépendante, on pourrait estimer l'équation de régression : $p(x,y,z) = \sum_{i,j,k}^{order}{c_{i,j,k}*x^i*y^j*z^k}$. La régression polynomiale est courante dans les cas où l'on veut détecter une certaine curvilinéarité dans une relation. Il s'agit essentiellement de la même idée que la régression linéaire multivariée dans un ordre supérieur.

np.polynomial.polynomial.polygrid3d
np.polynomial.polynomial.polyval3d

Mesure des performances et choix de la méthode

La quantification des distances perceptuelle, ΔE 2000 , a été utilisée pour évaluer l’efficacité des transformations utilisées. Le calcul des ΔE 2000 sur les correctifs de la cible commerciale a permis de déterminer le modèle susceptible de fournir les meilleurs résultats lors de la validation. Le calcul des ΔE 2000 sur les carrés de la cible personnalisée a été utilisé pour la

$\Delta E_{00} = \sqrt{(\frac{\Delta L'}{k_L S_L})^2 + (\frac{\Delta C'}{k_C S_C})^2 + (\frac{\Delta H'}{k_H S_H})^2 + R_T \frac{\Delta C'}{k_C S_C} \frac{\Delta H'}{k_H S_H} }$

Où $R_T$ est la matrice de rotation des couleurs, $S_L$, $S_C$ et $S_H$ terme correspondent respectivement à la luminance, à la compensation chromatique et à la compensation des couleurs. Lorsque $\Delta E_{00} = 1$ la couleur est la même \dots Le résultat a été testé sur l'original détecté avec un supplément de $\mathbf{10\%}$ de bruit gaussien aléatoire à l'intérieur d'un espace couleur différent.

Resultats

Les distances perceptuelles ont ete extraites et montre une amélioration significative de la correction des couleurs, le bruit supplémentaire de $10\%$ correspond à la valeur de $5,2$ de l'équation précédente. On peut voir leur correction respective dans l'espace rgb dans les images en annexe.

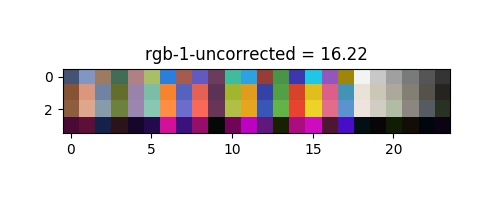
Les colonnes "non corrigées" montrent une différence minuscule, et signifient une perte de précision lors de la conversion des couleurs. Le meilleur espace semble etre l'espace $rgb$ a partir de ces premiers resultats, ce qui signifie que le déplacement du zéro (zéro n'est pas centré) dans les autres espaces ($lab, hsv, xyz$) ajoute un biais lors de l'ajustement, plus l'erreur de conversion des couleurs. On peu exclure dans un premier temps l'espace $hsv$ et les methodes rigid et poly qui montre tout deux de mauvais resultats voir empire la situation. De plus, la figure suivante montre les méthodes proposées dans différents espaces de couleur :

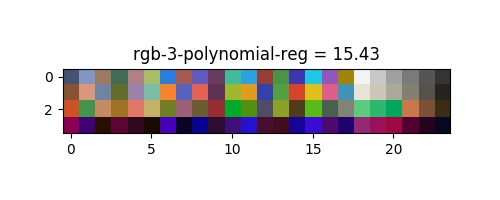
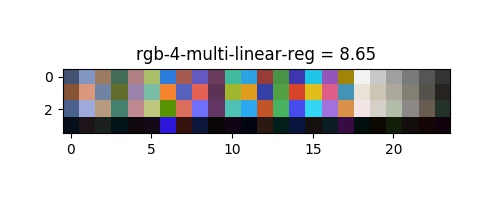
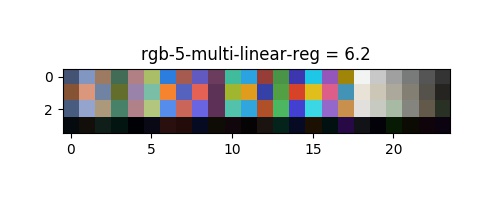
La transformée rigide fournit le résultat attendu (intéressant seulement pour comparer d'autres algorithmes), il corrige surtout la balance des blancs, et une certaine rotation à l'intérieur de l'espace qui n'est pas suffisante pour modéliser la relation des transferts de couleurs. On peut voir un ajustement trop contraint pour la regression polynomial, à moins que le résultat soit bon sans bruit, le modèle montre le pire résultat. D'après l'article de G. D. Finlayson and M. Mackiewicz and A. Hurlbert les régression linéaire multiple montrent un bon résultat qui pourrait être suffisant. Notre proposition de régression polynomiale multivariée montre le meilleur résultat dans presque tout les espaces qui est presque parfait : $6,4-5,2 = 1,2 \approx 1$, où 1 est une correction parfaite, les 0,2 restants sont négligeables et ne peuvent être perçus par l'œil humain. La metrique a elle seul n'est pas suffisant pour selectionner la bonne methode et le bon espace, car nous pouvons constater une perte du «blanc» dans les espaces $rgb$ et $xyz$. l'espace $lab$ montre dans le cas multi-lin une erreur bleu et dans le cas multi-poly une saturation trop importante.

Pour conclure, il semblerais donc que l'espace $yuv$ soit le plus appropriees ! Les deux methode multi-lin et multi-poly presente tout deux de bon resultats, avec une preference pour multi-poly en terme de metrique. Ces deux methodes semble egalement plus robuste au transfert sur des donnees reel (les chevres). Puisque bien que le model rigid montre une metrique acceptable, l'application sur les chevres est errone.

Annexe :