L’idée principale de l’apprentissage contrastif est d’apprendre des représentations (espace d’intégration) telles que les échantillons similaires restent proches les uns des autres, tandis que les échantillons dissemblables sont éloignés. L’apprentissage contrastif peut être appliqué à des contextes supervisés et non supervisés. Lorsqu’on travaille avec des données non supervisées, l’apprentissage contrastif est l’une des approches les plus intéressantes. Il a été démontré qu’il permettait d’obtenir de bonnes performances dans une variété de tâches de vision et de langage. Pour réaliser cet apprentissage, on a recours à des fonctions de pertes spécifiques.

Dans le contexte de la vision par ordinateur, une paire d’images est considérée comme un exemple positif si elle est similaire (par exemple, de la même classe d’objets) et comme un exemple négatif si elle est dissemblable (par exemple, de classes d’objets différentes). L’apprentissage contrastif vise à apprendre une représentation d’une image qui est similaire à celle d’un exemple positif et dissemblable à celle d’un exemple négatif. L’idée clé est que si nous pouvons apprendre une telle représentation, elle devrait être utile pour la classification (supervisée et non-supervisée).

L’apprentissage contrastif est généralement formulé comme une tâche de classification par paires. Étant donné un lot de données non étiquetées, nous cherchons à apprendre une représentation $ z_i $ de chaque échantillon de données $ x_i $. Pour apprendre une telle représentation, nous devons d’abord définir une fonction de similarité $ sim_{im}(x_i, x_j) $ qui mesure la similarité entre $ x_i $ et $ x_j $. La fonction de similarité est généralement définie sur la base de la distance entre $ x_i $ et $ x_j $. Par exemple, la distance euclidienne peut être utilisée comme fonction de similarité dans l’apprentissage contrastif euclidien. Mais bien d’autres fonctions de similarité sont possibles et grâce à cette fonction de similarité ainsi qu’une heuristique pour définir $ x_i $ et $ x_j $, de nombreuses fonctions de perte ont été imaginées, certaines sont introduites ici, bien que de nombreuses aient été proposées dans la littérature:


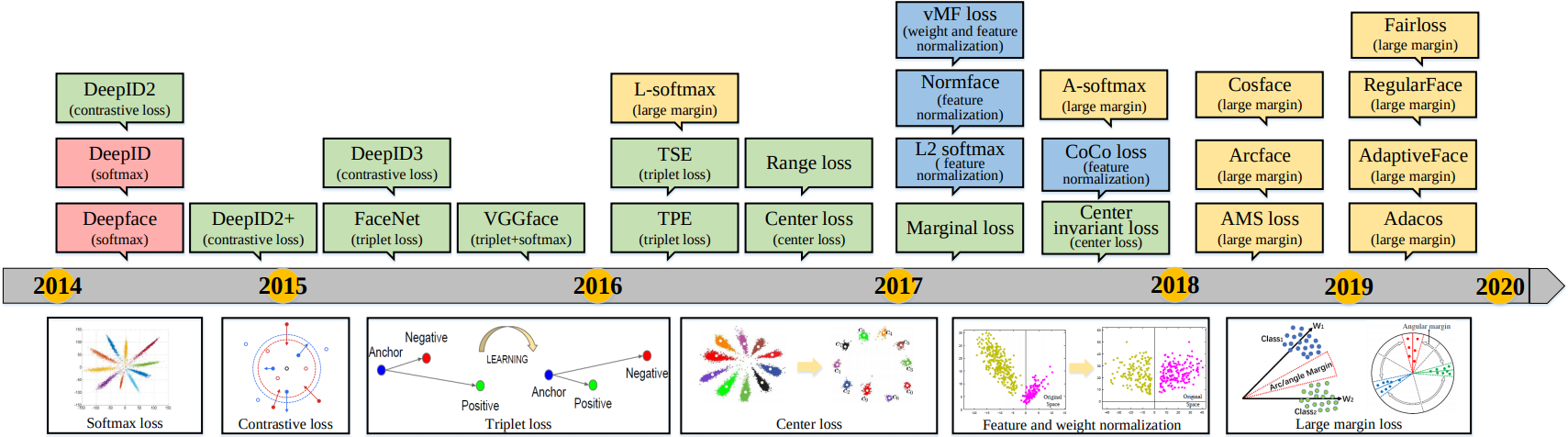
Historique des fonctions de perte contrastive pour DeepFace
(source: Wang 2019)

Contrastive Loss

Contrastive loss (Chopra et al. 2005) est l’une des premières fonctions de perte utilisées pour l’apprentissage de métriques profondes. Étant donné une liste d’échantillons d’entrée $ {x_i} $, où chaque échantillon possède une étiquette $ y_i \in { 1, \ldots, L } $ parmi $ L $ classes, on souhaite apprendre une fonction $ f_\theta(): X \to \mathbb{R}^d $ qui encode $ x_i $ dans un espace latent tel que les exemples de la même classe soient rapprochés, et que les échantillons de classes différentes soient éloignés.

La fonction de perte contrastive prend une paire d’entrées $ (x_i, x_j) $ et minimise la distance dans cet espace lorsqu’ils appartiennent à la même classe, mais maximise la distance sinon. Pour cette fonction de perte, on utilise habituellement la distance euclidienne. Ainsi, on cherche à minimiser la distance $D_{ij} = \left| f_\theta(x_i) - f_\theta(x_j) \right|_2^2$ lorsque les échantillons sont dans la même classe, et à maximiser cette distance lorsqu’ils sont dans des classes différentes.

$$ L_{cont}(\mathbf{x}_i, \mathbf{x}_j, \theta) = \mathbb{1}[y_i = y_j] D_{ij} + \mathbb{1}[y_i \neq y_j] \max(0, \epsilon - D_{ij}) $$

où $\epsilon$ est un hyperparamètre, définissant la distance minimale entre les échantillons de classes différentes.


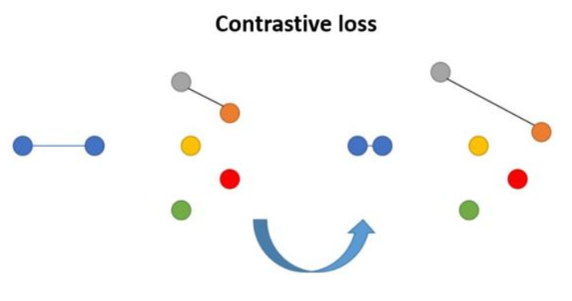
Illustration de la fonction de perte contrastive.
(Image source: Medela 2019) 

def criterion(x1, x2, label, margin=1.0):
    dist = torch.nn.functional.pairwise_distance(x1, x2)
    positive = (1 - label) * torch.pow(dist, 2)
    negative = (label) * torch.pow(torch.relu(margin - dist), 2)
    return torch.mean(positive + negative)

Triplet Loss

Triplet loss a été proposée à l’origine dans l’article FaceNet (Schroff et al. 2015) et a été utilisée pour apprendre la reconnaissance des visages d’une même personne dans différentes poses et sous différents angles.


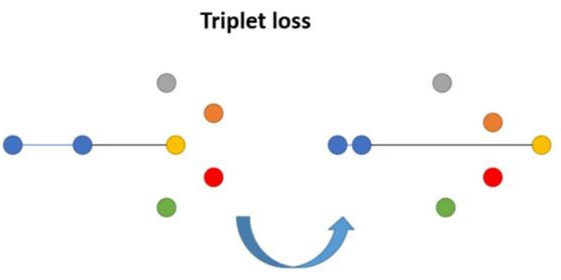
Illustration de la fonction de perte triplet compte tenu d'un positif et d'un négatif par rapport à l'ancre.
(Image source: Medela 2019)

Étant donné une entrée d’ancrage $ x $, nous sélectionnons un échantillon positif $ x^+ $ et un négatif $ x^- $, c’est-à-dire que $ x^+ $ et $ x $ appartiennent à la même classe, tandis que $ x^- $ provient d’une autre classe. La fonction de perte triplet apprend à minimiser la distance positive (entre $ x $ et $ x^+ $) et à maximiser la distance négative (entre $ x $ et $ x^- $) en même temps, selon l’équation suivante :

$$ L_{triplet}(\mathbf{x}, \mathbf{x}^+, \mathbf{x}^-) = \sum_{\mathbf{x}\in\mathcal{X}} \max\left( 0, \|\!| f(x) - f(x^+) \|\!|_2^2 - \|\!| f(x) - f(x^-) \|\!|_2^2 + \epsilon \right) $$

où le paramètre de marge $ \epsilon $ représente le décalage minimum entre les distances des paires similaires et dissemblables, one parle aussi de hard margin. Il est crucial de sélectionner des $ x^- $ “difficiles” pour améliorer le modèle, c’est-à-dire des $ x^- $ très proches de $ x $, engendrant des confusions; en pratique, cette sélection se fait souvent aléatoirement. Dans le cas de la triplet loss pour la réidentification, il a été proposé de lisser la fonction de perte afin d’éviter certains minima locaux et obtenir un espace latent plus robuste, on parle alors de soft margin :

$$ L_{triplet}(\mathbf{x}, \mathbf{x}^+, \mathbf{x}^-) = \sum_{\mathbf{x}\in\mathcal{X}} \log \left[ 1 + \exp\left( \|\!| f(x) - f(x^+) \|\!|_2^2 - \|\!| f(x) - f(x^-) \|\!|_2^2 + \epsilon \right) \right] $$ 

def criterion(anchor, positive, negative, margin=1.0):
    distance_positive = (anchor - positive).pow(2).sum(1)
    distance_negative = (anchor - negative).pow(2).sum(1)
    losses = torch.nn.functional.relu(distance_positive - distance_negative + margin)
    return losses.mean()

Lifted Structured Loss

Lifted Structured Loss (Song et al. 2015) utilise toutes les paires d’arêtes dans un lot (batch) pour une meilleure efficacité computationnelle (temps et erreur).


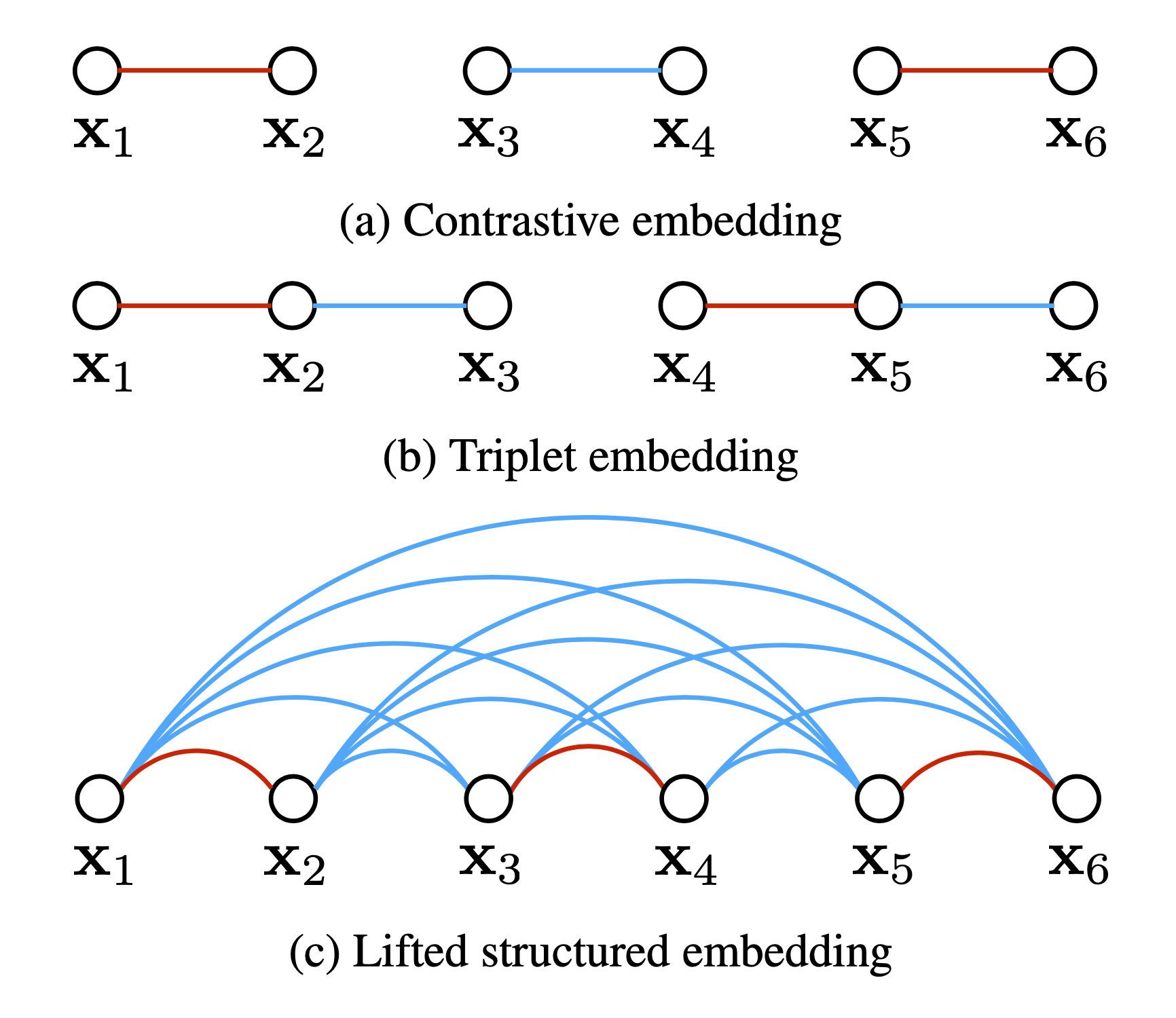
L'illustration compare la perte contrastive, la triplet loss et la lifted structured loss.
Les arcs rouges et bleus relient respectivement les paires d'échantillons similaires et différentes.
(Image source: Song et al. 2015)

Soit $D_{ij} = \left| f(\mathbf{x}_i) - f(\mathbf{x}_j) \right|_2$ la matrice des distances quadratique entre chaque paire, la fonction de perte structurée levée est définie comme suit :

$$\begin{aligned} \mathcal{L}_\text{struct} &= \frac{1}{2 \mathcal{P}} \sum_{(i,j) \in \mathcal{P}} \max(0, \mathcal{L}_\text{struct}^{(ij)})^2 \\ \text{where } \mathcal{L}_\text{struct}^{(ij)} &= D_{ij} + \underbrace{\max \big( \max_{(i,k)\in \mathcal{N}} \epsilon - D_{ik}, \max_{(j,l)\in \mathcal{N}} \epsilon - D_{jl} \big)} \end{aligned}$$

où $P$ contient l’ensemble des paires positives et $N$ est l’ensemble des paires négatives. La partie souligné de $L_\text{struct}(i, j)$ est utilisée pour l’extraction des négatifs (hard margin). Cependant, elle n’est pas lisse et peut entraîner la convergence vers un mauvais optimum local dans la pratique. Ainsi, elle est lissé (soft margin) pour devenir :

$$\mathcal{L}_\text{struct}^{(ij)} = D_{ij} + \log \Big( \sum_{(i,k)\in\mathcal{N}} \exp(\epsilon - D_{ik}) + \sum_{(j,l)\in\mathcal{N}} \exp(\epsilon - D_{jl}) \Big)$$

Dans cet article, ils ont également proposé d’améliorer la qualité des échantillons négatifs dans chaque lot en incorporant activement des échantillons négatifs difficiles étant donné des paires positives aléatoires.

def criterion(score, target, margin=1.0):
    loss, counter = 0, 0
    bsz = score.size(0)

    mag = (score ** 2).sum(1).expand(bsz, bsz)
    sim = score.mm(score.transpose(0, 1))
    dist = (mag + mag.transpose(0, 1) - 2 * sim)
    dist = torch.nn.functional.relu(dist).sqrt()

    for i in range(bsz):
        t_i = target[i].data[0]
        for j in range(i + 1, bsz):
            t_j = target[j].data[0]
            if t_i == t_j:
                l_ni = (margin - dist[i][target != t_i]).exp().sum()
                l_nj = (margin - dist[j][target != t_j]).exp().sum()
                l_n  = (l_ni + l_nj).log()
                l_p  = dist[i,j]
                loss += torch.nn.functional.relu(l_n + l_p) ** 2
                counter += 1

    return loss / (2 * counter)

N-pair Loss

Improved Deep Metric Learning with Multi-class N-pair Loss Objective (Sohn 2016) généralise la fonction de perte triplet pour inclure la comparaison avec des échantillons négatifs multiples. Étant donné les exemples d’apprentissage composés de $N+1$ éléments, ${\mathbf{x}, \mathbf{x}^+, \mathbf{x}1^-, \dots, \mathbf{x}^-}$, dont un positif et des négatifs, la fonction de perte N-pair est définie comme suit :

\[ \begin{aligned} \mathcal{L}_\text{N-pair}(\mathbf{x}, \mathbf{x}^+, \{\mathbf{x}^-_i\}^{N-1}_{i=1}) &= \log\big(1 + \sum_{i=1}^{N-1} \exp(f(\mathbf{x})^\top f(\mathbf{x}^-_i) - f(\mathbf{x})^\top f(\mathbf{x}^+))\big) \\ &= -\log\frac{\exp(f(\mathbf{x})^\top f(\mathbf{x}^+))}{\exp(f(\mathbf{x})^\top f(\mathbf{x}^+)) + \sum_{i=1}^{N-1} \exp(f(\mathbf{x})^\top f(\mathbf{x}^-_i))} \end{aligned} \]

Si un seul échantillon négatif par classe est pris, cela correspond à un softmax pour la classification multi-classes.


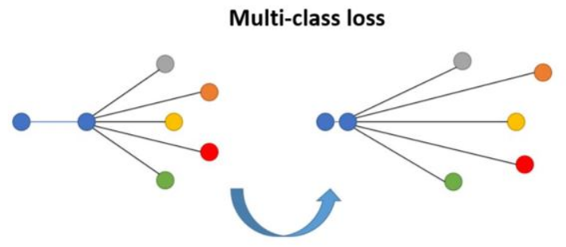
Illustration de la fonction de perte N-pair.
1 distance positive et N distances négatives sont considérées
(Image source: Medela 2019) 

def criterion(anchor, positive, l2_reg=0.02):
    batch_size = anchor.size(0)
    logit = torch.matmul(anchor, torch.transpose(positive, 0, 1))
    logit = torch.exp(logit - torch.diag(logit))
    loss_ce = torch.log(torch.sum(logit, dim=1)).mean()
    l2_loss = torch.sum(anchor**2) / batch_size + torch.sum(positive**2) / batch_size
    return loss_ce + self.l2_reg * l2_loss * 0.25

Constellation Loss

Constellation Loss: Improving the efficiency of deep metric learning loss functions for optimal embedding (Medela 2019)

La perte par constellation prend le meilleur de la loss par triplet et la loss N-pair multiclasses. Elle utilise la même construction de lot que la triplet loss, et une formulation similaire à la N-pair multiclasses. L’hyperparamètre K définit le nombre de triplets incorporés, permettant de prendre en compte plus de termes négatifs qu’avec la loss triplet standard. Même si augmenter K implique plus de calculs, il a été prouvé que dans certains cas, augmenter K n’affecte plus les résultats à partir d’un certain seuil, notamment en raison du caractère aléatoire du choix des négatifs. La principale différence : la N-pair multiclasses soustrait les produits scalaires des paires de même classe, tandis que la constellation loss soustrait le produit scalaire entre une ancre et un négatif, et celui entre une ancre et un positif.


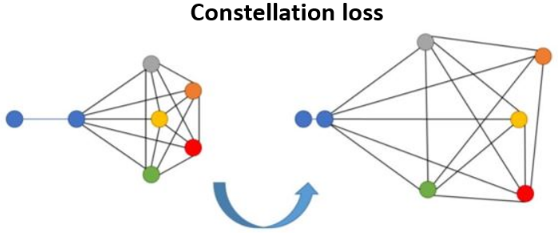
Illustration de la fonction de perte Constelation
Toutes les combinaisons sont considérées
(Image source: Medela 2019) 

def criterion(anchors, positives, negatives, target):
    num_class = len(np.unique(target))
    n = triplets.shape

    anchors = torch.unsqueeze(anchors, dim=1)
    positives = torch.unsqueeze(positives, dim=1)
    negatives = torch.unsqueeze(negatives, dim=1)
    x = torch.matmul(anchors, (negatives - positives).transpose(1,2))
    x = torch.exp(x.squeeze())
    x = torch.sum(torch.reshape(x, (num_class, -1)), axis=1)
    loss = torch.log(1 + x)

    return loss.mean()

Label Aware Ranked Loss

La fonction LARL prend en entrée un ensemble d’étiquettes de vérité terrain et un ensemble de scores prédits pour chaque étiquette. Elle calcule une perte de classement pour chaque étiquette en se basant sur la différence entre le score prédit et celui de l’étiquette incorrecte la mieux classée. Cette perte est multipliée par un facteur de pondération dépendant de la position de l’étiquette correcte dans le classement.

Formellement, la fonction LARL est définie comme suit :

$$ LARL = \sum_{i=1}^{N} w_i \max(0, m - s_{y_i} + s_{j^*}) $$

où :

  • $N$ est le nombre d’étiquettes,
  • $w_i$ est le facteur de pondération de l’étiquette $i$,
  • $m$ est un hyperparamètre de marge,
  • $s_{y_i}$ est le score prédit pour l’étiquette de vérité terrain $y_i$,
  • $s_{j^*}$ est le score de l’étiquette incorrecte la mieux classée.

Le facteur de pondération $w_i$ est défini comme :

$$ w_i = \left(1 + \log(1 + c^* n_i)\right)^{-1} $$

où :

  • $c$ est un hyperparamètre qui contrôle la force de la pondération,
  • $n_i$ est le nombre d’exemples possédant l’étiquette $i$,
  • $\log$ est la fonction logarithme naturel.

La fonction $LARL$ encourage le modèle à classer plus haut les étiquettes correctes que les étiquettes incorrectes pour une entrée donnée, et peut ainsi améliorer la performance globale sur des tâches de classification multi-labels.

Magnet Loss

La fonction de perte Magnet a été proposée dans Metric Learning with Adaptive Density Discrimination. Au lieu d’opérer sur des individus, des paires ou des triplets de données, Magnet Loss fonctionne sur des régions entières de l’espace d’intégration occupées par les points de données. La fonction modélise les distributions des différentes classes dans cet espace et s’efforce de réduire le chevauchement entre ces distributions.


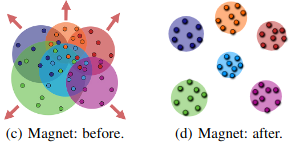
Illustration de la fonction de perte magnétique
(Image source: Rippel 2016)

Quelques ressources et implémentations :

  • https://github.com/pumpikano/tf-magnet-loss
  • https://github.com/mbanani/pytorch-magnet-loss