Introduction

La théorie des graphes concerne de nombreux domaines d’application, leurs objectifs sont différents mais le langage utilisé est le même. Les graphes sont utilisés pour modéliser des ensembles structurés, complexes, avec de nombreuses applications, telles que la modélisation dans le temps (en économie ou automatique) ou dans des réseaux divers (électrique, routier, adduction d’eau, …). La théorie des graphes est née en 1736 quand Euler démontra qu’il était impossible de traverser chacun des 7 ponts de la ville russe de Könisberg - Kaliningrad - Калининград une fois exactement et de revenir au point de départ :

De manière générale, un graphe permet de représenter simplement la structure, les cheminements possibles dans un grand nombre de situations en exprimant les relations et les dépendances entre les éléments. Par exemple dans un réseau ferroviaire, un arbre généalogique, le diagramme de succession de tâches en gestion… etc. En plus de son existence purement mathématique, le graphe est aussi une structure de données en informatique, les applications sont nombreuses et indispensables pour résoudre bon nombre de problèmes d’optimisation.

Théorie des graphes et conflits de brevets

Ce graphique illustre les relations juridiques entre plusieurs grandes entreprises du secteur technologique, principalement autour de conflits de brevets. On y observe des poursuites judiciaires fréquentes, notamment entre Apple, Samsung, Microsoft, et Motorola, souvent en lien avec les technologies mobiles. Microsoft adopte une stratégie mixte, combinant poursuites et accords de licence, tandis que Kodak, très actif dans les litiges, a aussi résolu plusieurs différends. Le graphique met en lumière l’intensité des guerres de brevets dans les années 2010, où la propriété intellectuelle était au cœur des stratégies concurrentielles.

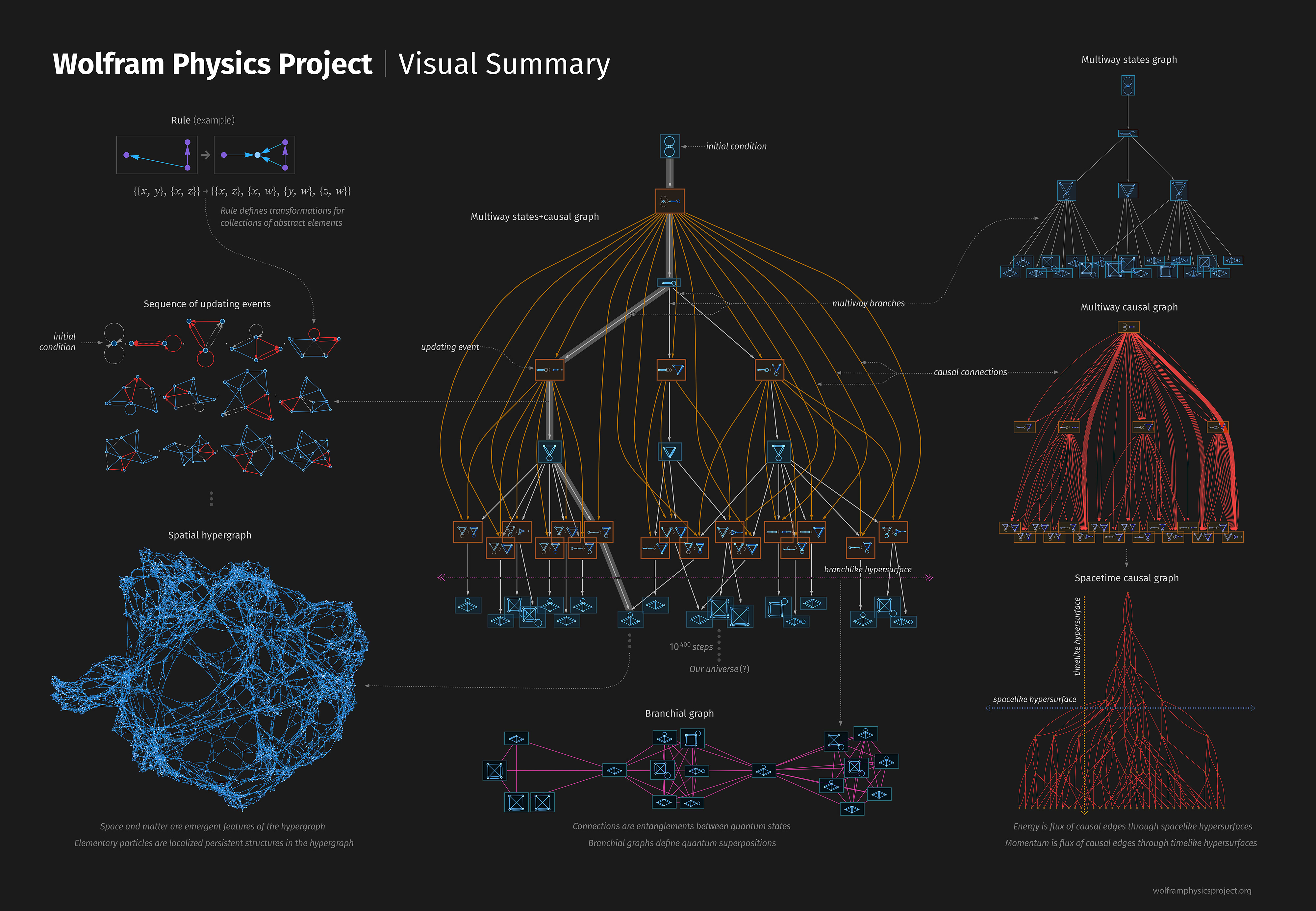
Rapprochement avec la physique - Projet Wolfram

Selon le Wolfram Physics Project, l’univers lui-même peut être modélisé comme un hypergraphe évolutif, chaque événement physique représentant une mise à jour dans le graphe. Les concepts de courbure, de causalité et d’entrelacement quantique y sont formalisés grâce à des graphes particuliers comme les causal graphs et branchial graphs, où les sommets et arêtes incarnent des événements et leurs relations causales.

Concept orienté

Dans beaucoup d’applications, les relations entre les éléments d’un ensemble sont orientées. Un élément $x$ peut être en relation avec un autre élément $y$ sans que $y$ ne soit nécessairement en relation avec $x$, dans ce cas on pourras parler de graph orienté ou encore de digraph. Pour formalisé un graph, on notera ce dernier $G=(X,U)$ qui est déterminé par :

• Un ensemble fini $X = {X_1, X_2, …, X_n}$ dont les éléments sont appelés sommets (ou nœuds).
  Si \$X\$ possède \$n\$ éléments distincts, le graphe est dit d’ordre $n$. On parle aussi de n-graphe. Les éléments de $X$ peuvent être nommés ou associés à une valeur.
• Un ensemble fini $U = {U_1, U_2, …, U_m}$ dont les éléments sont des couples ordonnés de sommets, appelés arcs. \$U\$ est donc une sous-famille du produit cartésien $X \times X = {(x, y) \mid x \in X, y \in X}$, dont les éléments sont les arcs du graphe. Pour un arc $u = (X_i, X_j)$, $X_i$ est le nœud initial (ou origine) et $X_j$ le nœud final (ou destination). Un arc $u = (X_i, X_i)$ est appelé une boucle, car le nœud initial et le nœud final sont identiques. Nous verrons plus tard que les arcs peuvent être nommés pour définir les relations entre objets, ou associés à une valeur (ou poids de transition).
• Un $p$-graphe est un graphe dans lequel il n’existe jamais plus de $p$ arcs de la forme $(X_i, X_j)$ entre deux sommets quelconques.

Suposont les ensembles $X = {A, B, C, D, E}$ et $U = {(A,B), (B,A), (A,D), (A,C), (A,E), (C,D), (C,E), (C,D), (B,C)}$. Le graphe résultant est le suivant :

Attention les notations anglais sont légèrement différentes :

Concept	Notation française	Nom en français	Notation anglaise	Nom en anglais
Ensemble de sommets	\$X\$	Sommets / Nœuds	\$V\$	Vertices / Nodes
Un sommet individuel	\$X_i\$	Sommet / Nœud	\$v_i\$	Vertex / Node
Ensemble d’arcs	\$U\$	Arcs	\$E\$	Edges (orienté : arcs)
Un arc individuel	\$(X_i, X_j)\$	Arc (orienté)	\$(v_i, v_j)\$	Edge / Arc
Arc non orienté	\${X_i, X_j}\$	Arête (non orientée)	\${v_i, v_j}\$	Edge (undirected)

Monograph (p=1)

• Chaque paire de sommets a au maximum une arête
• Équivaut à un graphe simple classique
• Pas d’arcs multiples entre les mêmes sommets

Exemple :

Également un 1-graph :

Également un 1-graph :

source : Catharine A Baker - 2002

Bigraph (p=2)

• Permet jusqu’à deux arêtes entre deux sommets
• Les arêtes peuvent être dans des sens opposés
• Utilisé pour représenter des relations bidirectionnelles

Exemple :

Également un 2-graph :

Multigraph (p>2)

• Plusieurs arêtes parallèles autorisées
• Représente des relations multiples entre sommets
• Utiles pour modéliser des systèmes complexes

Exemple 3-graph (p=3):

source : Catharine A Baker - 2002

Applications multivoques

L’application $\Gamma$ qui à tout élément de $X$ fait correspondre une partie de $X$ est appelée une application multivoque :

• $X_j$ est le successeur de $X_i$ si le couple $(X_i, X_j) \in U$.
  L’ensemble des successeurs de $X_i$ est noté $\Gamma(X_i)$.
• $X_j$ est le prédécesseur de $X_i$ si le couple $(X_j, X_i) \in U$.
  L’ensemble des prédécesseurs de $X_i$ est noté $\Gamma^{-1}(X_i)$.

Exemple 1

• $X = {x_1, x_2, x_3, x_4, x_5}$
• $\Gamma(x_1) = {x_2}$
• $\Gamma(x_2) = {x_1, x_3}$
• $\Gamma(x_3) = {x_4, x_5}$
• $\Gamma(x_4) = {x_5}$
• $\Gamma(x_5) = {x_1, x_2}$

Déduction de $W^{+}$ (arcs sortants) :

• $W^{+}(x_1) = {(x_1, x_2)}$
• $W^{+}(x_2) = {(x_2, x_1), (x_2, x_3)}$
• $W^{+}(x_3) = {(x_3, x_4), (x_3, x_5)}$
• $W^{+}(x_4) = {(x_4, x_5)}$
• $W^{+}(x_5) = {(x_5, x_1), (x_5, x_2)}$

Déduction $W^{-}$ (arcs entrants) :

• $W^{-}(x_1) = {(x_2, x_1), (x_5, x_1)}$
• $W^{-}(x_2) = {(x_1, x_2), (x_5, x_2)}$
• $W^{-}(x_3) = {(x_2, x_3)}$
• $W^{-}(x_4) = {(x_3, x_4)}$
• $W^{-}(x_5) = {(x_3, x_5), (x_4, x_5)}$

Exemple 2

• $X = {x_1, x_2, x_3, x_4, x_5}$
• $\Gamma^{-1}(x_1) = {x_1, x_3}$
• $\Gamma^{-1}(x_2) = {x_1, x_4}$
• $\Gamma^{-1}(x_3) = {x3, x_4, x_5}$
• $\Gamma^{-1}(x_4) = {x_2, x_1}$
• $\Gamma^{-1}(x_5) = {x_3, x_5}$

Graphes non orientés

Lors de l’étude de certaines propriétés, il arrive que l’orientation des arcs ne joue aucun rôle. On s’intéresse uniquement à l’existence d’arcs entre deux sommets sans que l’ordre ne soit précisé. On appelle arête tout arc sans orientation. L’ensemble $U$ est alors constitué de paires de sommets non ordonnées.

• On dit que $u$ est incident au sommet pour une arête $(X_i, X_j)$.
• Pour les graphes non orientés, on note souvent $G = (X, E)$ et $e = [X_i, X_j]$.
• Un multi-graphe $G = (X, E)$ est un graphe dans lequel il existe plusieurs arêtes entre deux sommets.

Exemple identique