Avant d’aborder les algorithmes d’optimisation ou les heuristiques de parcours, il est indispensable de maîtriser les représentations structurelles d’un graphe et les propriétés algébriques qui en découlent. Ce cours fixe ainsi quatre objectifs : (1) savoir encoder un graphe par matrices ou par listes ; (2) calculer et interpréter le degré d’un sommet ainsi que la connexité globale ; (3) reconnaître un graphe biparti sous ses diverses facettes ; (4) interpréter le spectre des matrices associées. Les sections qui suivent reprennent et complètent le support que vous avez déjà rédigé, en y ajoutant des exemples codés, des illustrations et un premier contact avec la théorie spectrale des graphes.
Représentation d’un graphe
Il existe plusieurs types de représentation pour décrire un graphe. On distingue principalement la représentation par matrice d’adjacence, par matrice d’incidence sommet-arcs et par liste d’adjacences.
Matrice d’adjacence
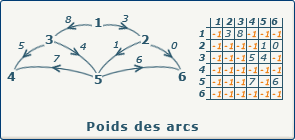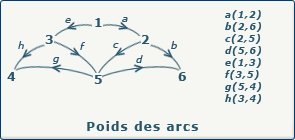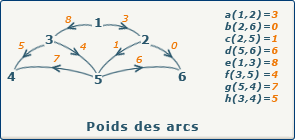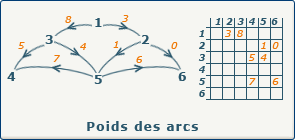
Pour un 1-graphe, la matrice d’adjacence fait correspondre les sommets origine des arcs (classés en ligne) aux sommets destination (classés en colonne).
Dans un formalisme matriciel booléen, l’existence d’un arc $(x_i,x_j)$ se traduit par la présence d’un 1 à l’intersection de la ligne $x_i$ et de la colonne $x_j$, et l’absence par un 0.
Dans un autre formalisme, la valeur correspond à un poids de transition sur l’arc ; s’il n’existe pas d’arc, le poids est fixé à $-1$.
C’est l’une des représentations les plus utilisées.
Par exemple, on peut simplement utiliser une matrice NumPy pour ce type de représentation :
n = 4 # number_of_nodes
connection = np.zeros((n, n))
connection[0, 0] = 1 # boucle sur x_1
connection[0, 2] = 1 # arc de x_1 -> x_3
# etc ...
Matrice d’incidence sommet-arc
Pour établir cette matrice, les lignes sont constituées des sommets du graphe et les colonnes des arcs.
On pose la valeur 1 pour le sommet d’origine et -1 pour le sommet de destination.
Encore une fois, une simple matrice NumPy peut être utilisée. Cependant, ce type de représentation est moins flexible à la modification (ajout/suppression d’arcs plus coûteux).
n = 2 # number_of_nodes
m = 1 # number_of_arcs
connection = np.zeros((n, m))
connection[0, 0] = -1 # arc de x_1
connection[1, 0] = 1 # vers x_2
Liste d’adjacence
L’objectif ici est de représenter chaque arc par son extrémité finale, l’extrémité initiale étant définie implicitement.
Tous les arcs émanant d’un même sommet sont liés dans une liste.
À chaque arc sont associés le sommet de destination et un pointeur vers le suivant.
Pour un 1-graphe, la représentation par liste d’adjacence est avantageuse (application \$\Gamma\$) car elle permet un gain de mémoire par rapport à la matrice d’adjacence, donc mieux adaptée à l’implémentation.

La représentation par liste d’adjacence nécessite la création de deux tableaux :
- \$LP\$ (ListePointeur) de dimension \$n+1\$
- \$LS\$ (ListeSuccesseurs) de dimension \$m\$ (pour graphes orientés) ou \$2m\$ (pour graphes non orientés)
Pour chaque sommet \$i\$, la liste des successeurs est contenue dans le tableau \$LS\$ à partir de l’indice \$LP[i]\$.
Les informations du sommet \$i\$ se trouvent dans les cases \$LS[LP[i]]\$ à \$LS[LP[i+1]-1]\$.
- \$w^{+}(i) = LP[i+1] - LP[i]\$ (orienté ou non-orienté)
- \$LP[i] = 1 + \sum_{j=1}^{i-1}{w^{+}(j)}\$
Cette représentation revient à décrire le graphe par son application multivoque \$i \rightarrow \Gamma(i)\$.
- Construire \$LS\$ par \$\Gamma(1), \Gamma(2), …, \Gamma(n)\$
- Construire \$LP\$ qui donne, pour chaque sommet, l’indice dans \$LS\$ où commence la liste de successeurs
- Pour le sommet \$i\$, son premier suivant est \$LS[LP[i]]
, le second $LS[LP[i]+1], etc.
L’ensemble est dans l’intervalle $[LP[i], LP[i+1]-1]\$ - Si un sommet \$i\$ n’a pas de successeur, on pose \$LP[i] = LP[i+1]`.
La liste est vide et coincée entre les successeurs de \$i-1\$ et \$i+1\$.
La place mémoire utilisée est \$n^2\$ pour un graphe d’ordre \$n\$.
Cependant, plusieurs implémentations sont possibles.
Une version plus simple et plus flexible en Python :
nodes = [[] for _ in range(number_of_nodes)]
nodes[0] = [1] # successeurs de x_1
nodes[1] = [0, 2] # successeurs de x_2
nodes[2] = [0, 1, 4]
nodes[3] = [2]
nodes[4] = [5]
nodes[5] = [2, 5] # boucle locale
Cependant, ce type de représentation ne permet pas de modéliser directement le poids des arcs.
Il faut ajouter un tableau supplémentaire, similaire à \$LS\$, pour contenir les poids.
On peut aussi aller plus loin en utilisant des classes.
Voir aussi jerryyin.info