
Abstract
Les indices colorimétriques en télédétection ont un large domaine d’application pour caractériser différents types de surface. Bien souvent, les formes d’indices de télédétection sont définies empiriquement, que ce soit en sélection des longueurs d’onde, de la forme de l’équation, ou des coefficients dans l’équation permettant de calculer le dit indice. Et un très petit nombre d’études optimisent les paramètres utilisés pour ces indices. Ces indices sont alors utilisés tel-quel pour de la classification (souvent linaire comme les RandomForest). Mais aucune étude ne semble chercher la meilleure forme de façon automatique afin d’optimiser la classification et/ou la segmentation.
Notons qu’il est important d’optimiser l’indice en amont, car la transformation engendre une perte d’information et de caractéristique essentielle à la classification.
Un “mauvais indice” ne permet donc pas une bonne classification, pour pallier à cet effet les études privilégie presque toujours l’utilisation de plusieurs indices et de méthode de classification avancée
Le site www.indexdatabase.de référence ces différents indices (choix des longueurs d’ondes et des coefficients) en fonction du matériel d’acquisition. Souvent, le dit matériel est satellitaire (Landsat-5) donc moins influencé par les différences de luminosité, ce qui pose des soucis dans d’autres applications telles qu’en proxy-détection ce qui est notre cas.
L’approche standard pour sélectionner l’indice qui correspond le mieux a ce que l’on cherche a caractériser consiste a tester tous les indices disponibles en fonction de nos longueurs d’ondes avec une simple corrélation entre les indices et une vérité terrain Svitlana Kokh. Ce n’est pas une mauvaise approche, mais elle reste sous-optimal et fastidieuse, car elle nécessite de coder l’ensemble des indices et leurs différentes versions et le niveau de corrélation n’est pas le meilleur estimateur.
Ainsi, l’objectif de cette étude est de développer une méthode de recherche de l’indice optimal grâce à une approche statistique par descente de gradient, sur différentes formes d’équation générique. Nous allons également tester de nouvelles approches par traitement du signal et analyse d’image. L’apprentissage est effectué à travers des mécanismes de deep-learning Tensorflow 2.0.
À titre d’illustration, l’indice le plus utilisé pour la végétation est NDVI qui offre une mean_iou de $72.7\%$, tandis que les “meilleurs” indices empiriques offre une mean_iou au mieux de $82.3\%$, la ou nos des formes d’indice généré automatiquement propose une mean_iou de $87\%$. Cette différence est suffisamment significative pour améliorer la segmentation et la robustesse de l’indice a différents facteurs extérieurs, ainsi que la forme des éléments détectée.
Materiel
Les images ont été acquises grâce à la caméra multispectrale à six bandes Airphen. C’est une caméra scientifique multispectrale développée par des agronomes pour des applications agricoles. Elle peut être intégrée dans différents types de plates-formes telles que des drones, des robots de phénotypage, etc.
La caméra a été configurée en utilisant les bandes 450/570/675/710/730/850 nm avec un FWHM de 10 nm. La focal de chaque objectif est de 8 mm. Leurs résolutions brutes, pour chaque bande spectrale sont de 1280x960 px avec une précision de 12 bits. Enfin, l’appareil est équipé d’une antenne GPS interne, qui peut être utilisée pour obtenir la distance par rapport au sol.
L’alignement est affiné en deux étapes, avec (i) une estimation approximative de l’enregistrement affine et (ii) un enregistrement en perspective pour le raffinement et la précision grâce à la détection et la mise en correspondance de points clé. La méthode utilisée pour l’enregistrement est basée sur des travaux antérieurs Two-step Multi-spectral Registration, où la méthode montre une précision de l’enregistrement jusqu’au sous-pixel.
Données
Les données ont été acquises sur le site de l’IRSTEA de Montoldre, dans l’Allier (03), en France dans le cadre de l’ANR Challenge Rose.
12 images présentant des caractéristiques très distinctes en terme d’illumination (ombre, matin, soir, plein soleil, nuageux, …) ont été acquises.
Ainsi 3 vérités terrain ont été définies :
Attention : cet article correspond à de premiers travaux sur le sujet en utilisant des images prises en bonnes conditions.
Des résultats complémentaires sont disponibles dans la publication disponible ici.
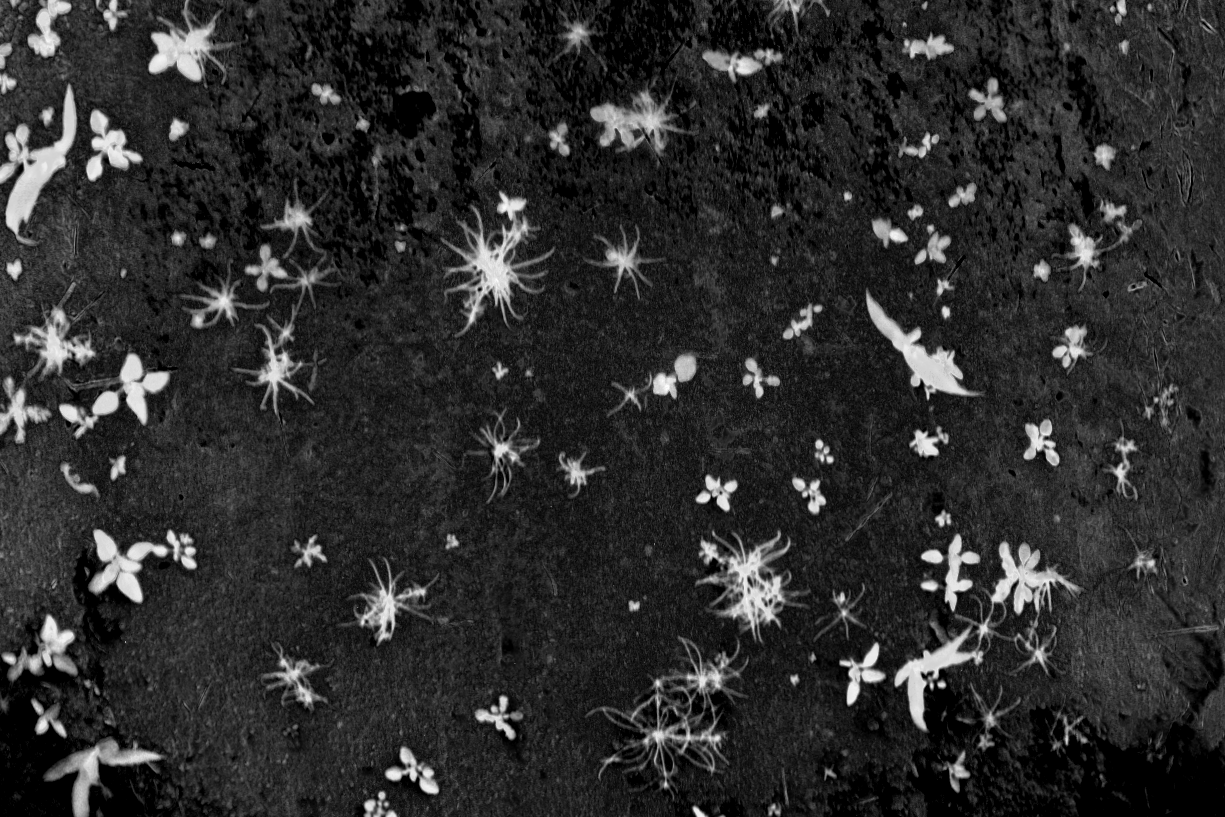
Exemple pour la végétation :
| Image originale | Masque |
|---|---|
 |
 |
@Article{rs13122261,
AUTHOR = {Vayssade, Jehan-Antoine and Paoli, Jean-Noël and Gée, Christelle and Jones, Gawain},
TITLE = {DeepIndices: Remote Sensing Indices Based on Approximation of Functions through Deep-Learning, Application to Uncalibrated Vegetation Images},
JOURNAL = {Remote Sensing},
VOLUME = {13},
YEAR = {2021},
NUMBER = {12},
ARTICLE-NUMBER = {2261},
URL = {https://www.mdpi.com/2072-4292/13/12/2261},
ISSN = {2072-4292},
DOI = {10.3390/rs13122261}
}
Pré-traitement de l’information
Les bandes spectrales présentent par nature un bruit important associé au capteur CCD, ce qui pose des soucis lors de la normalisation.
Pour pallier à cet effet, 1% du signal minimum et maximum est supprimé par le calcul des quantiles, puis chaque bande est normalisée dans l’intervalle $[0,1]$.
Nous ajoutons également quelques transformations des bandes spectrales afin d’enrichir le pool d’information et de prendre en compte les gradients dans l’image.
Le choix s’est orienté vers 5 informations importantes :
- L’image de la déviation standard entre toutes les bandes $\lambda_{dev}$
- Le gradient via un filtre de Sharr sur $\lambda_{dev}$ noté $\lambda_{grad}$
- Les valeurs propres maximales de la matrice Hessienne de $\lambda_{dev}$ notées $\lambda_{ridge_{max}}$
- Les valeurs propres minimales de la matrice Hessienne de $\lambda_{dev}$ notées $\lambda_{ridge_{min}}$
- Le laplacien de $\lambda_{dev}$ noté $\lambda_{laplace}$
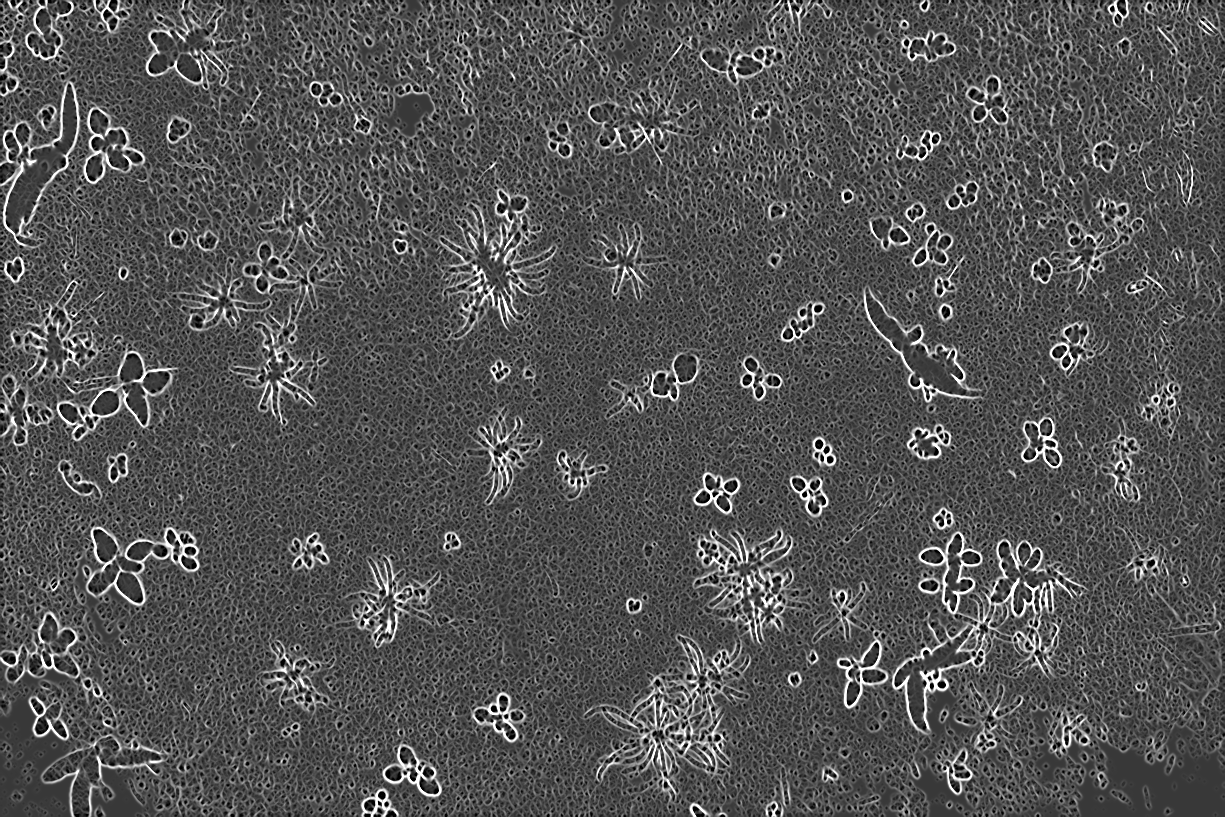
| Déviation standard | Filtre de Sharr | Valeurs propres max | Valeurs propres min | Laplacien |
|---|---|---|---|---|
 |
 |
 |
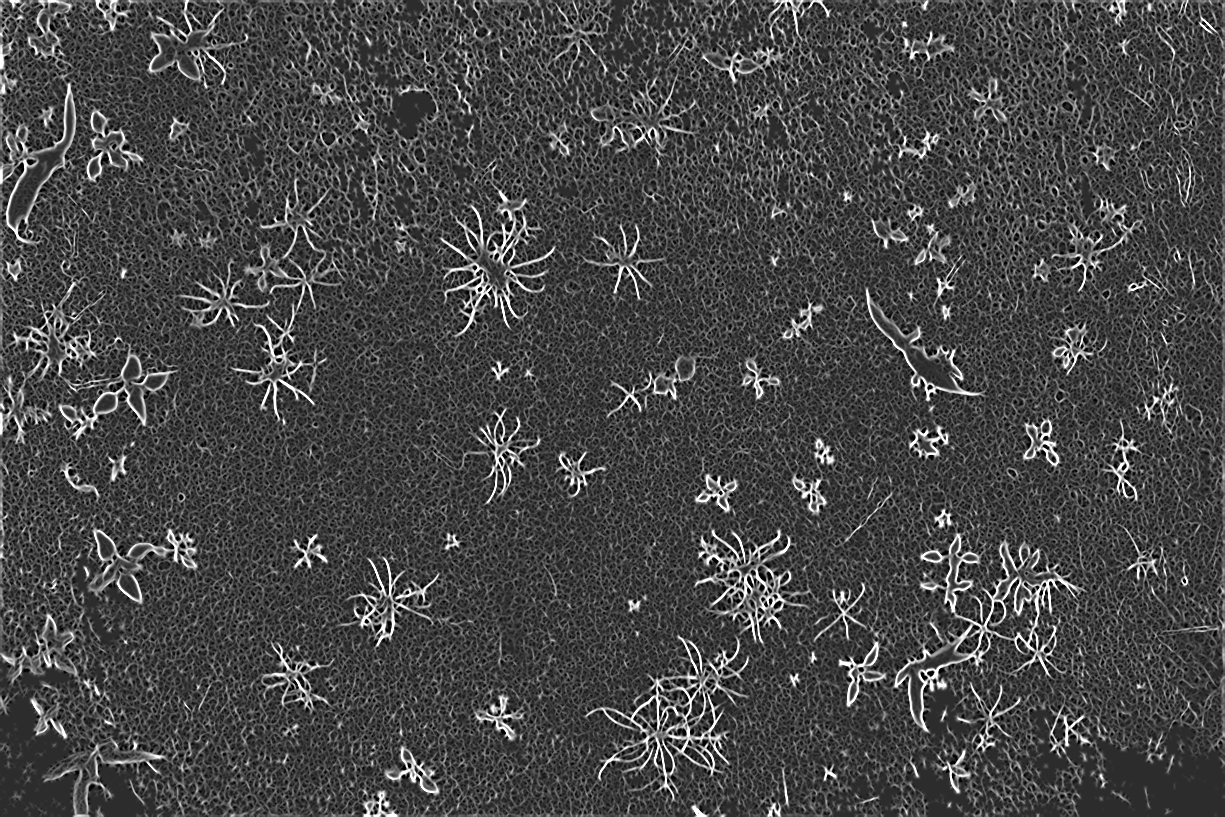 |
 |
En effet, ces 5 transformations offrent d’une part une information importante sur le mélange spectral grâce à la déviation standard. Le filtre de Sharr et les valeurs propres maximum donne une information spatiale importante sur la rupture des gradients, donc sur la limite extérieure des objets, ce qui aidera probablement a la convergence. Les valeurs propres minimum, aussi appeler ridge, quant à elle semble détecté facilement les éléments fins tels que les monocotylédones pour des images de végétations.
Indices et forme d’équation
Les indices colorimétriques ont prouvé leur efficacité dans la description des surfaces, ainsi tous les ans différents articles de revue concernant les indices colorimétriques sortent, souvent dans le cadre d’un premier article de thèse appliqué à un domaine d’étude spécifique (Xue Jinru, Çağatay Tanrıverdi, Jiri Mezera). Nous allons repartir de la base grâce au site www.indexdatabase.de, à partir de cette base de données, 89 indices de végétation ont été identifiés comme compatibles avec nos longueurs d’ondes, ils seront ainsi testés. D’autre part, ils seront comparés à nos indices conçus automatiquement. Six formes d’équations simples ont été extraites à partir de l’ensemble des 519 indices de la base de données :
| # | Titre | Équation |
|---|---|---|
| 1 | Une seule bande | $I = \lambda_i$ |
| 2 | Soustraction de bande | $I = \lambda_i - \lambda_j$ |
| 3 | Différence de 2 bandes | $I = \lambda_i / \lambda_j$ |
| 4 | Différence normalisée de 2 bandes | $I = \frac{\lambda_i - \lambda_j}{\lambda_i + \lambda_j}$ |
| 5 | Différence normalisée de 3 bandes | $I = \frac{2\lambda_i - \lambda_j - \lambda_k}{2\lambda_i + \lambda_j + \lambda_k}$ |
| 6 | Différence normalisée “cubique” de 2 bandes | $I = \frac{\lambda_i - \lambda_j}{\sqrt{\lambda_i + \lambda_j}}$ |
En analysant ces différentes équations, nous pouvons définir de nouvelles formes d’équation générique qui les synthétisent, et qui prennent en compte l’ensemble des bandes spectrales ainsi qu’un certain voisinage. Deux autres formes d’équations sont également intéressantes à optimiser, qui sont respectivement les approximations de fonction continue par développement de Taylor, ainsi que les approximations de fonction continue par morceaux grâce aux opérateurs morphologiques. Ces équations seront alors optimisées permettant de définir de nouveaux indices automatiquement, dans la seconde partie. L’ensemble de ces méthodes est développé via TensorFlow et les paragraphes suivants présentent les différents modèles :
Linéaire : Pour synthétiser les équations 1 et 2, nous pouvons définir une simple équation linéaire telle que $I = \sum_{i=0}^{N}{\alpha_i \lambda_i}$. Cette équation peut se généraliser au domaine 2D par une Convolution avec dans sa forme simple une taille de noyaux $k=1,1$.
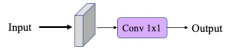
Différence Linéaire : Pour synthétiser les équations 3, 4 et 5, un modèle simple reposant sur une division de deux modèles précédents est possible. De la même façon, cette forme est généralisable au domaine 2D et correspond alors à deux Convolution2D, l’une pour le numérateur, l’autre pour le dénominateur. Nous fixons dans un premier temps la taille des noyaux à $k=1,1$ pour ne pas prendre en considération le voisinage. Nous avons utilisé l’opérateur “nan div” pour remplacer les résultats “not a number” par zéro.
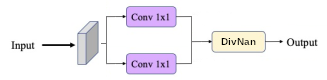
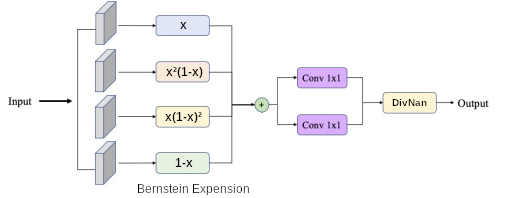
Polynomial : D’après le théorème de Stone–Weierstrass, toute fonction continue définie sur un segment peut être approchée uniformément par des fonctions polynomiales. Puisque l’on restreint le segment au domaine [0-1], les polynômes de Bernstein en sont une démonstration commune. Ainsi, toutes formes d’indices colorimétriques peut être approximée par un polynôme $I = \sum_{i=0}^{N}{\alpha_i \lambda_i}^{\delta_i}$. Pour des raisons d’implémentations, deux opérateurs sont définis. D’une part l’exposant $\lambda_i^\delta$, puis l’équation linéaire définie par une Convolution2D pour garder la possibilité de l’étendre au domaine 2D.

Différence Polynomial : En suivant l’idée de la forme précédente et pour respecter la forme d’équations 6, nous introduisons simplement une différence de polynôme, l’un au numérateur permettant d’optimiser la classe recherchée et l’autre au dénominateur jouant le rôle de normalisateur $\frac{\sum_{i=0}^{N} \alpha_i \lambda_i ^ {\delta_i} + A} {\sum_{j=0}^{N} \alpha_j \lambda_j ^ {\delta_j} + B}$. (voir les réultats si pertinant -> puisque thérème de StoneWeierstrass)
Approximation Universelle de Fonction : En utilisant les développements de Taylor, nous pouvons décomposer n’importe quelle fonction $f(x)$ en $f(x) = f(0) + f’(x) x + \frac{1}{2} f’‘(x) x^2 + \frac{1}{6} f’‘’(x) x^3 + o(x^3)$. Une approche pour apprendre cette forme de développement est proposée par Huang et al., 2017 que l’on appelle communément DenseNet et correspond alors à la somme de la concaténation du signal et de ses dérivées $\mathbf{x} \to \left[\mathbf{x}, f_1(\mathbf{x}), f_2(\mathbf{x}, f_1(\mathbf{x})), f_3(\mathbf{x}, f_1(\mathbf{x}), f_2(\mathbf{x}, f_1(\mathbf{x})), \ldots\right]$. Les dérivées sont disponibles par l’utilisation d’une Convolution2D.
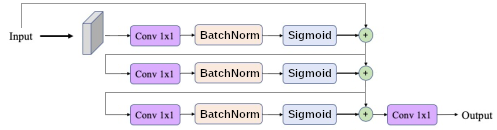
https://d2l.ai/chapter_convolutional-modern/densenet.html
Filtre d’entrée : Pour supprimer une partie du signal qui ne serait pas indispensable, nous étudierons l’ajout d’un filtre passe-bande, en amont du réseau. Effectivement, pourquoi prendre en considération l’ensemble des valeurs d’un signal ? Il est très probable que seulement une partie de ce dernier caractérise ce que l’on cherche. Un bon exemple concerne les indices de végétation, seules les valeurs fortes dans le vert et le proche infra-rouge, ainsi que les valeurs faibles dans le rouge et le bleu sont caractéristiques de la végétation :

Note : C’est d’ailleurs le principe de l’indice NDVI, en raison des couches spongieuses qui se trouvent sur leur face arrière, les feuilles réfléchissent beaucoup de lumière dans le proche infrarouge, ce qui contraste fortement avec la plupart des objets non-végétaux. Lorsque la plante est déshydratée ou stressée, la couche spongieuse se compresse et les feuilles réfléchissent moins de lumière dans le proche infrarouge, rejoignant les valeurs du rouge, dans le domaine visible. Ainsi, la combinaison mathématique de ces deux signaux peut aider à différencier les plantes des objets non-végétaux et les plantes saines des plantes malades. Cependant, cet indice est alors moins intéressant lorsqu’il s’agit de détecter seulement la végétation et est fortement influencé par l’ombrage ou la chaleur.
Nous allons donc ajouter un filtre dans les équations précédentes pour supprimer les valeurs “indésirables” par l’utilisation de deux seuils a et b, qui seront également appris. S’il s’avère que l’ensemble du signal est intéressant, ces deux paramètres ne changeront pas et les valeurs seront a=0 et b=1, dans le cas contraire, a et b changeront. Pour appliquer le premier seuil, on utilise l’équation $y = \max(x-a,0) \div (1-a)$ et permet donc de supprimer les valeurs basses. À partir de ce nouveau signal, on applique l’équation $z = \max(b-y,0) \div b$ pour supprimer les valeurs hautes.
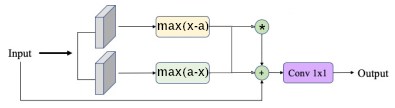
Ces deux paramètres permettent aussi de gérer des paramètres extérieurs, en effet lorsque a devient négatif, le paramètre a pour effet de rehausser le signal, ce dernier est alors compris dans l’intervalle $[a,1]$. Le second paramètre b permet par exemple de supprimer les effets de spéculaires ou de bruit trop important.
Approximation de fonction par érosion-dilatation : En étendant l’idée de sélection de bandes, nous pouvons non pas en sélectionner une, mais plusieurs, grâce à des opérateurs morphologiques notés $x \oplus s = \max_k(x_k + s_k)$ et $x \ominus s = \max_k(s_k - x_k)$ avec $x_k$ les différentes bandes spectrales et les $s_k$ le coefficient d’érosion de la bande spectrale $\ominus$ ou de dilatation $\oplus$. En augmentant le nombre d’érosion-dilatation, c’est-à-dire, en définissant plusieurs $s_k$ noté $s_{k,i}$, nous pouvons approximer n’importe quelle fonction continue par morceaux (Ranjan Mondal). On pose alors $z_i^{+} = x \oplus s_i = \max_k(x_k + s_{k,i})$ qui est le neurone structurant de dilatation $i$ et $z_i^{-} = x \ominus s_i = \max_k(s_{k,i} - x_k)$ qui est le neurone structurant d’érosion. Pour obtenir la sortie $I = \sum_{i=0}^{N}{z_i^{+}w_i^{+}} + \sum_{i=0}^{N}{z_i^{-}w_i^{-}}$ dont les $w_i^{+}$ et les $w_i^{-}$ sont les coefficients de combinaison linéaire obtenue par Convolution 2D pour rester dans le domaine 2D.
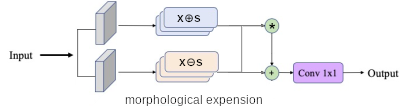
Raffinement spatial de l’indice : Pour prendre en compte différentes échelles dans l’image, nous étudions l’ajout d’une partie en aval du réseau. Appelé “Spatial Pyramide Refinement Block” et consiste en la somme de différentes Convolution2D dont les tailles de noyaux ont été fixées à 1,3,5,7. Le résultat de chaque convolution est concaténé, et le résultat final est donné par une combinaison linéaire de ces différentes échelles modélisées encore une fois par une Convolution2D avec k=1.
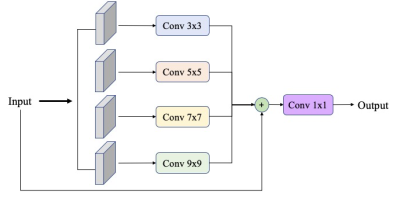
Fonction de perte
Dans cette partie, nous présenterons les différentes fonctions de pertes possibles en relation à la classification binaire. Cette partie est inspirée de https://lars76.github.io/neural-networks/object-detection/losses-for-segmentation/. Pour obtenir un indice et faciliter la convergence, on s’intéressera uniquement aux valeurs comprises entre 0 et 1 en sortie de la dernière couche, via une fonction d’activation de type ClippedReLU ($0<=x<=1$), ce qui est négatif ou nul sera donc indésirable et supérieur ou égal à 1 la classe recherchée et entre les deux la frontière d’indécision à optimiser. Les valeurs correspondent alors à la probabilité que le pixel soit la surface recherchée $P(Y=1)=1=p$ ou non $P(Y=0) = 1-p$. Dans ce cas, 4 fonctions sont communément utilisées : Cross-Entropy, Weigthed-Cross-Entropy, Balanced-Cross-Entropy et Focal-Loss (dans la suite nous noterons $p$ la vérité terrain et $\hat{p}$ la prédiction).
Cross-Entropy : La cross-entropy peut être définie par $CE(p,\hat{p}) = -p\log(\hat{p}) -(1-p)\log(1-\hat{p})$. C’est une fonction de perte standard qui ne prend pas en compte le ratio des classes (unbalanced). Elle permet de mesurer la séparabilité des classes. Lorsque $CE \rightarrow 0$ il n’y a plus d’entropie et $\hat{p} \rightarrow p$, dans le cas contraire, si $CE \rightarrow 1$ alors $\hat{p}$ et $p$ sont indissociables. La fonction de perte $CE$ ne semble pas être adaptée à notre cas, puisque l’on utilise une vérité terrain dont le ratio entre surface recherchée et le reste, des différences pour chaque image.
Weigthed-Cross-Entropy : C’est une variante de $CE$ où tous les membres de classes positive ($p=1$) sont pondérés par un coefficient $\beta$, lequel permet de réguler le ratio des classes. On écrit alors $WEC(p,\hat{p}) = -\beta p\log(\hat{p}) -(1-p)\log(1-\hat{p})$. Pour décrémenter l’effet de la classe $Y=0$ on fixe $\beta>1$ et $\beta<1$ dans le cas contraire. Le coefficient $\beta$ peut être fixé pour maximiser une classe spécifique, ou contrebalancer le ratio des classes. Le coefficient $\beta$ pourrait néanmoins être calculé indépendamment pour chaque image.
Balanced-Cross-Entropy : Cette variante est similaire à WCE, on introduit cependant $1-\beta$ pour la classe négative. On a donc l’équation $BCE(p,\hat{p}) = -\beta p\log(\hat{p}) -(1-\beta)(1-p)\log(1-\hat{p})$. Cette forme est intéressante, puisque $\beta$ peut soit être fixé comme pour $WCE$, soit être calculé pour chaque image, dans ce cas $\beta = \sum(\frac{P(Y=1)}{P(Y=0)})$.
Focal Loss : Cette fonction, proche de BCE essaie de décrémenter l’influence des éléments “faciles” pour améliorer en priorité les éléments difficilement séparables. On utilise alors deux coefficients $\alpha$ et $\gamma$ sur la distribution de $\hat{p}$. La fonction s’écrit alors $FL(p,\hat{p}) = -(\alpha (1-\hat{p})^\gamma) p\log(\hat{p}) -(1-\alpha)\hat{p}^\gamma(1-p)\log(1-\hat{p})$. La fonction de perte $FL$ ne permet pas de prendre en considération le ratio des classes différents pour chaque image. La fonction ne permet pas d’optimiser l’indice dans l’intervalle [0-1] avec efficacité et donc l’optimisation des métriques définis plus loin. Bien que le coefficient $\alpha$ puisse être calculé automatiquement, le coefficient $\gamma$ est difficile à fixer.
Trois autres fonctions de perte sont intéressantes à étudier quand il s’agit de segmentation : Dice-Loss, TverskyIndex-Loss et IntersectionOverUnion-Loss souvent utilisés dans leurs versions métrique.
Dice-Loss : La fonction de perte est définie par $\text{DL}(p, \hat{p}) = 1 - \frac{2p\hat{p}}{p + \hat{p}}$
IntersectionOverUnion-Loss : Récemment, Y.Wang et al ont proposé une solution pour optimiser une approximation de l’intersection sur l’union dans le cas de segmentation binaire. La fonction de perte est définie par $IoU = 1 - \frac{I(p, \hat{p})}{U(p, \hat{p})}$ avec $I(p, \hat{p}) = p\hat{p}$ et $U(p, \hat{p}) = p+\hat{p} - p\hat{p}$. Les performances de cette fonction de perte semblent plus efficaces que les méthodes “simples” précédemment citées (Gellért Máttyus, Dingfu Zhou, Zhaohui Zheng).
Le choix se fera donc sur la fonction de perte $BCE$ avec un calcul automatique de $\beta$.
Métrique d’évaluation
Lorsque le nombre d’éléments entre chaque classe est fortement déséquilibré, beaucoup de métriques standard sont inefficaces et donc inadaptées. Par exemple, notre vérité terrain sol/végétation comporte ~83% de sol et donc ~17% de végétation, une mauvaise métrique comme l’accuracy montrera de “bonnes” performances. Dans le cas de l’accuracy $\frac{tp+tn}{tp+tn+fp+fn}$ si l’évaluation ne détecte que du sol alors les performances seront de ~83% ce qui n’est donc pas représentatif. Ce que l’on cherche alors est de trouver des métriques permettant de prendre en compte le ratio de chaque classe. Communément, les performances des indices colorimétriques est calculée par une cross-entropy $-\frac{1}{N} \sum_{i=0}^{N}{y_{true}\log(y_{pred}) + (1-y_{true})\log(1-y_{pred})}$ entre l’indice et une vérité terrain. Comme nous l’avons vu précédemment, cette métrique n’est pas non plus adaptée car elle ne prend pas en compte le ratio des classes. Il existe beaucoup d’autres métriques (Abdel Aziz, David Martin Ward Powers, Takaya Saito, László A. Jeni) :
Balanced Accuracy : Aussi appelé Youden Statistics pour prendre en compte le ratio des classes, la forme de l’accuracy est transformée afin de calculer séparément les performances de chaque classe et devient donc $\frac{1}{2}(\frac{tp}{tp+fp} + \frac{tn}{tn+fn})$
Dice : Le coefficient de Dice, également appelé indice de recouvrement, est communément utilisé pour vérifier les performances des algorithmes de segmentation $\frac{2p\hat{p}}{p+\hat{p}}$
Mean Intersection Over Union : C’est une autre métrique souvent utilisée pour mesurer les performances de la segmentation, notée $\frac{p\hat{p}}{p+\hat{p} - p\hat{p}}$
Precision : Correspond à une partie de l’équation de balanced accuracy $\frac{tp}{tp+fp}$ et permet de répondre à la question : Quelle proportion des identifications positives a été effectivement correcte ?
Recall : Quelle proportion de vrais positifs a été identifiée correctement ? $\frac{tp}{tp+fn}$
Matthews correlation : $\frac{tptn - fpfn}{\sqrt((tp+fp)(tp+fn)(tn+fp)*(tn+fn))}$
Comparaison avec les indices standards
Pour effectuer une comparaison juste/équitable, il est nécessaire d’optimiser chaque indice standard. Pour ce faire, un réseau de neurones minimal est utilisé afin d’apprendre une droite de régression. Le réseau est donc composé de l’indice spectral, suivi d’une normalisation $x=(x-min)/(min-max)$, puis d’une convolution 2D avec une taille de noyau de $k=1,1$. Puisque l’indice génère une seule dimension, l’équation de sortie est alors $I = \alpha * NormalizedIndex + \beta$. Pour effectuer la classification de la même façon que notre méthode, une activation de type ClipedRelu est utilisée. Évidemment, les mêmes métriques et fonction de perte sont utilisées.

Réseau de neurones simple
| AdventicedTransformedSoilAdjustedVI | GlobalEnvironmentMonitoringIndex |
|---|---|
| AnthocyaninRefectanceIndex | GlobalVegetationMoistureIndex |
| AshburnVegetationIndex | GreenAtmosphericallyResistantVegetationIndex |
| AtmosphericallyResistantVegetationIndex2 | GreenBlueNDVI |
| AtmosphericallyResistantVegetationIndex | GreenLeafIndex |
| AverageReflectance750to850 | GreenNormalizedDifferenceVegetationIndex |
| BlueWideDynamicRangeVegetationIndex | GreenOptimizedSoilAdjustedVegetationIndex |
| BrowningReflectanceIndex | GreenRedNDVI |
| CanopyChlorophyllContentIndex | GreenSoilAdjustedVegetationIndex |
| ChlorophyllAbsorptionRatioIndex2 | IdealVegetationIndex |
| ChlorophyllAbsorptionRatioIndex | InfraredPercentageVegetationIndex |
| ChlorophyllGreen | Intensity |
| ChlorophyllIndexGreen | MCARI_OSAVI750 |
| ChlorophyllIndexRedEdge710 | MCARI_OSAVI |
| ChlorophyllIndexRedEdge | mCRIRE |
| ChlorophyllRedEdge | MisraGreenVegetationIndex |
| ChlorophyllVegetationIndex | MisraNonSuchIndex |
| ColorationIndex | MisraSoilBrightnessIndex |
| CorrectedTransformedVegetationIndex | MisraYellowVegetationIndex |
| CRI700 | ModifiedAnthocyaninReflectanceIndex |
| Datt1 | ModifiedChlorophyllAbsorptionInReflectanceIndex1 |
| Datt4 | ModifiedChlorophyllAbsorptionInReflectanceIndex |
| Datt6 | ModifiedSimpleRatio670_800 |
| DifferencedVegetationIndexMSS | ModifiedSimpleRatio705_750 |
| DifferenceNIRGreenVegetationIndex | ModifiedSimpleRatio |
| DoubleDifferenceIndex | ModifiedSoilAdjustedVegetationIndex |
| EnhancedVegetationIndex2 | ModifiedTriangularVegetationIndex1 |
| EnhancedVegetationIndex3 | mSR2 |
| EnhancedVegetationIndex | NDVI |
| Gitelson2 | NormG |
| NormNir | |
| NormR | |
| PanNDVI | |
| RedBlueNDVI | |
| RedEdgeInflectionPoint | |
| RedEdgePositionLinearInterpolation | |
| ShapeIndex | |
| SoilAdjustedVegetationIndex | |
| SoilAndAtmosphericallyResistantVegetationIndex2 | |
| SoilAndAtmosphericallyResistantVegetationIndex3 | |
| SoilAndAtmosphericallyResistantVegetationIndex | |
| SpecificLeafAreaVegetationIndex | |
| SpectralPolygonVegetationIndex | |
| StructureIntensivePigmentIndex1 | |
| StructureIntensivePigmentIndex2 | |
| TasselledCapNonSuchIndexMSS | |
| TasselledCapSoilBrightnessIndexMSS | |
| TasselledCapYellowVegetationIndexMSS | |
| TCARI_OSAVI | |
| TransformedChlorophyllAbsorbtionRatio2 | |
| TransformedChlorophyllAbsorbtionRatio | |
| TransformedNDVI | |
| TriangularChlorophyllIndex | |
| TriangularVegetationIndex | |
| VegetationConditionIndex | |
| VegetationIndex700 | |
| VisibleAtmosphericallyResistantIndexGreen | |
| VisibleAtmosphericallyResistantIndices700 | |
| WideDynamicRangeVegetationIndex |
Resultats sur les indices de végétations
Performance des indices généré (balanced-accuracy)
| model | none | ibf | sprb | ibf-sprb |
| linear-1 | 0.920456 | 0.957441 | 0.948547 | 0.959523 |
| linear-3 | 0.944438 | 0.953185 | 0.949021 | 0.948238 |
| linear-5 | 0.946792 | 0.948180 | 0.948658 | 0.952501 |
| linear-difference-1 | 0.931371 | 0.957029 | 0.950979 | 0.959641 |
| linear-difference-3 | 0.945933 | 0.953706 | 0.948506 | 0.947711 |
| linear-difference-5 | 0.946004 | 0.949275 | 0.946124 | 0.949065 |
| polynomial-1 | 0.851377 | 0.958745 | 0.932263 | 0.960028 |
| polynomial-3 | 0.926293 | 0.953239 | 0.946023 | 0.944787 |
| polynomial-5 | 0.940114 | 0.945173 | 0.952135 | 0.946668 |
| polynomial-difference-1 | 0.852644 | 0.941546 | 0.932263 | 0.960195 |
| polynomial-difference-3 | 0.925979 | 0.952306 | 0.949190 | 0.952061 |
| polynomial-difference-5 | 0.940247 | 0.946793 | 0.950396 | 0.946668 |
| universal-function-1 | 0.960796 | 0.956361 | 0.958163 | 0.961680 |
| universal-function-3 | 0.955876 | 0.960021 | 0.959222 | 0.957073 |
| universal-function-5 | 0.956568 | 0.957891 | 0.949323 | 0.955690 |
| dense-morphological-1 | 0.958957 | 0.961354 | 0.957494 | 0.954695 |
| dense-morphological-3 | 0.957006 | 0.960109 | 0.953354 | 0.947386 |
| dense-morphological-5 | 0.954817 | 0.956036 | 0.954024 | 0.947997 |
Performance des indices généré (dice)
| model | none | ibf | sprb | ibf-sprb |
| linear-1 | 0.897379 | 0.919146 | 0.908837 | 0.920147 |
| linear-3 | 0.905065 | 0.916038 | 0.908416 | 0.919359 |
| linear-5 | 0.905870 | 0.910275 | 0.908126 | 0.917741 |
| linear-difference-1 | 0.902534 | 0.918402 | 0.909899 | 0.920550 |
| linear-difference-3 | 0.906899 | 0.915144 | 0.908671 | 0.916320 |
| linear-difference-5 | 0.906015 | 0.911114 | 0.908691 | 0.916163 |
| polynomial-1 | 0.715673 | 0.918931 | 0.890213 | 0.920157 |
| polynomial-3 | 0.883776 | 0.915555 | 0.903123 | 0.916701 |
| polynomial-5 | 0.893659 | 0.906864 | 0.909151 | 0.918699 |
| polynomial-difference-1 | 0.715874 | 0.912215 | 0.890213 | 0.921199 |
| polynomial-difference-3 | 0.883730 | 0.914634 | 0.905640 | 0.918628 |
| polynomial-difference-5 | 0.893659 | 0.908827 | 0.907722 | 0.918699 |
| universal-function-1 | 0.921699 | 0.916650 | 0.918785 | 0.921204 |
| universal-function-3 | 0.915790 | 0.919687 | 0.919694 | 0.916641 |
| universal-function-5 | 0.916150 | 0.915613 | 0.910322 | 0.914890 |
| dense-morphological-1 | 0.916389 | 0.919247 | 0.920824 | 0.922081 |
| dense-morphological-3 | 0.914703 | 0.918109 | 0.919472 | 0.923553 |
| dense-morphological-5 | 0.912327 | 0.914024 | 0.918995 | 0.923483 |
Performance des indices généré (mean-iou) :
| model | none | ibf | sprb | ibf-sprb |
| linear-1 | 0.81701 | 0.85370 | 0.83547 | 0.85535 |
| linear-3 | 0.82911 | 0.84771 | 0.83462 | 0.85350 |
| linear-5 | 0.83033 | 0.83754 | 0.83413 | 0.85051 |
| linear-difference-1 | 0.82531 | 0.85236 | 0.83733 | 0.85602 |
| linear-difference-3 | 0.83215 | 0.84612 | 0.83510 | 0.84793 |
| linear-difference-5 | 0.83056 | 0.83904 | 0.83503 | 0.84762 |
| polynomial-1 | 0.57002 | 0.85320 | 0.80435 | 0.85541 |
| polynomial-3 | 0.79451 | 0.84673 | 0.82576 | 0.84861 |
| polynomial-5 | 0.80995 | 0.83156 | 0.83609 | 0.85213 |
| polynomial-difference-1 | 0.57025 | 0.84163 | 0.80435 | 0.85723 |
| polynomial-difference-3 | 0.79443 | 0.84520 | 0.83009 | 0.85212 |
| polynomial-difference-5 | 0.80995 | 0.83483 | 0.83363 | 0.85213 |
| universal-function-1 | 0.85812 | 0.84949 | 0.85302 | 0.85764 |
| universal-function-3 | 0.84762 | 0.85465 | 0.85436 | 0.84903 |
| universal-function-5 | 0.84814 | 0.84728 | 0.83786 | 0.84580 |
| dense-morphological-1 | 0.84892 | 0.85399 | 0.85672 | 0.85891 |
| dense-morphological-3 | 0.84580 | 0.85185 | 0.85379 | 0.86099 |
| dense-morphological-5 | 0.84156 | 0.84468 | 0.85294 | 0.86088 |
Performances des indices standars :
| model | mean_iou | dice | balanced_accuracy | precision | recall | matthews_correlation |
| TasselledCapSoilBrightnessIndexMSS | 0.8164615631 | 0.897600472 | 0.9235137105 | 0.9368506074 | 0.8546644449 | 0.8301048279 |
| EnhancedVegetationIndex2 | 0.8144683242 | 0.8967437148 | 0.925162077 | 0.9092102647 | 0.8797735572 | 0.8477547765 |
| ModifiedSoilAdjustedVegetationIndex | 0.8066384196 | 0.8919746876 | 0.919921875 | 0.9073579907 | 0.8724440336 | 0.8362452984 |
| EnhancedVegetationIndex3 | 0.8034334183 | 0.8899865746 | 0.9238960147 | 0.9103938341 | 0.8658408523 | 0.8410320878 |
| SoilAndAtmosphericallyResistantVegetationIndex3 | 0.801486671 | 0.8888103962 | 0.9164751172 | 0.9019806385 | 0.8715785742 | 0.8308723569 |
| SoilAdjustedVegetationIndex | 0.8014482856 | 0.8887869716 | 0.9162079692 | 0.9016042948 | 0.8718970418 | 0.8309013844 |
| MisraGreenVegetationIndex | 0.7969615459 | 0.8855116367 | 0.9290137887 | 0.9373131394 | 0.8317774534 | 0.8277327418 |
| AdventicedTransformedSoilAdjustedVI | 0.7866845131 | 0.8795798421 | 0.9075129628 | 0.8919116259 | 0.8636738658 | 0.8142505288 |
| GlobalEnvironmentMonitoringIndex | 0.7567619681 | 0.8594646454 | 0.9316999316 | 0.9518594146 | 0.7797127366 | 0.809997499 |
| SoilAndAtmosphericallyResistantVegetationIndex | 0.7673212886 | 0.8672993779 | 0.9186453223 | 0.8995713592 | 0.8325374126 | 0.8209629059 |
| SpectralPolygonVegetationIndex | 0.7610459924 | 0.8630498052 | 0.9089462757 | 0.8748332858 | 0.8507961035 | 0.8196647763 |
| ModifiedTriangularVegetationIndex1 | 0.7534039617 | 0.8584382534 | 0.9175352454 | 0.8952250481 | 0.8196260929 | 0.819590807 |
| ModifiedChlorophyllAbsorptionInReflectanceIndex1 | 0.7533426881 | 0.8584012985 | 0.9173633456 | 0.8947824836 | 0.8199580312 | 0.8195903897 |
| AshburnVegetationIndex | 0.7065967917 | 0.8256232142 | 0.8877642155 | 0.9357358217 | 0.7273611426 | 0.7371518016 |
| NDVI | 0.7246574759 | 0.8383700848 | 0.8718431592 | 0.800101757 | 0.8800880313 | 0.7832633853 |
| AtmosphericallyResistantVegetationIndex2 | 0.7255876064 | 0.8390240669 | 0.8753374219 | 0.7975414991 | 0.8848151565 | 0.7918048501 |
| RedBlueNDVI | 0.6982311606 | 0.8199477792 | 0.8583303094 | 0.8246154785 | 0.8154640794 | 0.7442476749 |
| InfraredPercentageVegetationIndex | 0.6959015727 | 0.8180093169 | 0.8659196496 | 0.8218980432 | 0.8130705953 | 0.747872591 |
| VegetationConditionIndex | 0.6839970946 | 0.8093613982 | 0.8529757857 | 0.8248573542 | 0.7933390737 | 0.7164512277 |
| VegetationIndex700 | 0.659373939 | 0.7928419113 | 0.885335207 | 0.8651016355 | 0.7308323383 | 0.7377569079 |
| DifferenceNIRGreenVegetationIndex | 0.6471098065 | 0.782320261 | 0.8600678444 | 0.8727560043 | 0.7149523497 | 0.6935585141 |
| AtmosphericallyResistantVegetationIndex | 0.6770561337 | 0.8034860492 | 0.8464117646 | 0.746306181 | 0.8684923053 | 0.7448039055 |
| GreenRedNDVI | 0.6498661041 | 0.7846027017 | 0.8224272132 | 0.7840580344 | 0.7874488235 | 0.6870804429 |
| SpecificLeafAreaVegetationIndex | 0.6190750003 | 0.7618000507 | 0.8194820285 | 0.7619611025 | 0.7661630511 | 0.6655799747 |
| GreenSoilAdjustedVegetationIndex | 0.5905128717 | 0.7388393283 | 0.8279193044 | 0.8056836724 | 0.6937674284 | 0.6463025212 |
| NormNir | 0.5951035023 | 0.7413546443 | 0.834320128 | 0.8029643297 | 0.691034615 | 0.6591392159 |
| VisibleAtmosphericallyResistantIndices700 | 0.5604120493 | 0.7159902453 | 0.8328130841 | 0.7463212609 | 0.6899870634 | 0.6619185209 |
| TransformedChlorophyllAbsorbtionRatio | 0.5139300823 | 0.6773368716 | 0.8335154653 | 0.7777052522 | 0.596609354 | 0.6187361479 |
| GreenLeafIndex | 0.4751126766 | 0.6409713626 | 0.8365080953 | 0.8406647444 | 0.5204018354 | 0.5822848678 |
| TriangularChlorophyllIndex | 0.4868407249 | 0.6529071927 | 0.7977802157 | 0.7446940541 | 0.5806494355 | 0.5728466511 |
| PanNDVI | 0.5621151328 | 0.7149507403 | 0.8048653603 | 0.6567967534 | 0.7964729667 | 0.665450573 |
| WideDynamicRangeVegetationIndex | 0.4400079548 | 0.5979006886 | 0.8667721748 | 0.821125567 | 0.4683559239 | 0.5846787095 |
| ModifiedChlorophyllAbsorptionInReflectanceIndex | 0.3894633353 | 0.5499406457 | 0.8392792344 | 0.8456571698 | 0.4269099236 | 0.5215582252 |
| ModifiedSimpleRatio670_800 | 0.4327640831 | 0.5955750346 | 0.816947937 | 0.7429494262 | 0.5245443583 | 0.5484391451 |
| TransformedChlorophyllAbsorbtionRatio2 | 0.3981522024 | 0.5662932992 | 0.7420825362 | 0.6672722101 | 0.5084164143 | 0.4585200846 |
| BlueWideDynamicRangeVegetationIndex | 0.3377201259 | 0.4973782599 | 0.8267631531 | 0.7540425658 | 0.3750333488 | 0.4852397442 |
| ModifiedSimpleRatio705_750 | 0.4228568375 | 0.5890919566 | 0.7497875094 | 0.6299832463 | 0.5710561275 | 0.5030774474 |
| mSR2 | 0.4316358864 | 0.5975112915 | 0.7513005137 | 0.6119061112 | 0.6031486988 | 0.5167066455 |
| GreenOptimizedSoilAdjustedVegetationIndex | 0.4525571167 | 0.6167977452 | 0.7414371967 | 0.600635469 | 0.6527581811 | 0.5271781087 |
| ModifiedAnthocyaninReflectanceIndex | 0.4354537725 | 0.6019610167 | 0.7592261434 | 0.6095924377 | 0.6030116677 | 0.5325561762 |
| ChlorophyllIndexRedEdge710 | 0.4320220649 | 0.5978645682 | 0.7557243705 | 0.6084275246 | 0.6073073745 | 0.5241049528 |
| GreenNormalizedDifferenceVegetationIndex | 0.4695614576 | 0.6330704093 | 0.743026495 | 0.5869406462 | 0.7083061934 | 0.5447127819 |
| ChlorophyllAbsorptionRatioIndex | 0.2096580416 | 0.3384151161 | 0.7801399231 | 0.9722483754 | 0.2129731774 | 0.3352024555 |
| ChlorophyllAbsorptionRatioIndex2 | 0.2095359117 | 0.3382484019 | 0.7807197571 | 0.9722768664 | 0.2128448337 | 0.3354943693 |
| GreenBlueNDVI | 0.479303211 | 0.6416514516 | 0.7858903408 | 0.5794430375 | 0.7396811843 | 0.6195572019 |
| ChlorophyllIndexGreen | 0.4296761453 | 0.5988509655 | 0.7546467781 | 0.5895750523 | 0.6247556806 | 0.5310488343 |
| DifferencedVegetationIndexMSS | 0.4806605875 | 0.6435986161 | 0.7237963676 | 0.5743008256 | 0.7282950878 | 0.5028678775 |
| NormR | 0.384023577 | 0.5422237515 | 0.7312939167 | 0.5876777172 | 0.5003208518 | 0.4259736538 |
| MisraYellowVegetationIndex | 0.2232471257 | 0.3568905592 | 0.6155403256 | 0.7171635032 | 0.2363708466 | 0.2159916312 |
| BrowningReflectanceIndex | 0.3565377891 | 0.5225743651 | 0.7159267068 | 0.5165106058 | 0.551173389 | 0.4472738206 |
| TriangularVegetationIndex | 0.4965699613 | 0.6582158208 | 0.7433443666 | 0.5066651702 | 0.9667960405 | 0.630377233 |
| TransformedNDVI | 0 | 0 | 0.4354068935 | 0 | 0 | 0 |
| CorrectedTransformedVegetationIndex | 0 | 0 | 0.4354068935 | 0 | 0 | 0 |
| IdealVegetationIndex | 0 | 0 | 0.4354068935 | 0 | 0 | 0 |
| AnthocyaninRefectanceIndex | 0.3368895352 | 0.5017370582 | 0.6936119199 | 0.4741534591 | 0.5543147326 | 0.4188344777 |
| SoilAndAtmosphericallyResistantVegetationIndex2 | 0.3948488235 | 0.5641175508 | 0.6997538209 | 0.4506566226 | 0.7800628543 | 0.496057272 |
| EnhancedVegetationIndex | 0.3950550258 | 0.5643129349 | 0.6996979713 | 0.4505939186 | 0.7810727358 | 0.4960843027 |
| Datt4 | 0.3611221015 | 0.5173488259 | 0.6305044293 | 0.4348393977 | 0.5972551107 | 0.3048333228 |
| DoubleDifferenceIndex | 0.1403269023 | 0.2408106178 | 0.5487119555 | 0.301677227 | 0.2071675956 | 0.0993415415 |
| CRI700 | 0.3215062022 | 0.4812051356 | 0.6659790874 | 0.4038533866 | 0.6043696404 | 0.3957900107 |
| mCRIRE | 0.0435240716 | 0.0828521475 | 0.5039966702 | 0.142893672 | 0.0600708909 | 0.0010207072 |
| Datt6 | 0.2247320265 | 0.3629664481 | 0.6129235625 | 0.3192526996 | 0.4265658855 | 0.2522099912 |
| ModifiedSimpleRatio | 0.0663518608 | 0.1237298548 | 0.5022712946 | 0.1423415542 | 0.1155181527 | 0.003576515 |
| GlobalVegetationMoistureIndex | 0.2471000403 | 0.390155673 | 0.5970597863 | 0.2962363064 | 0.5928331017 | 0.2595480382 |
| VisibleAtmosphericallyResistantIndexGreen | 0.261462301 | 0.4121804237 | 0.5958778262 | 0.3074308038 | 0.6589137912 | 0.2676194012 |
| TasselledCapYellowVegetationIndexMSS | 0.2188976854 | 0.3523357809 | 0.5846978426 | 0.2583462298 | 0.535658896 | 0.2193143815 |
| AverageReflectance750to850 | 0.234171629 | 0.3770784438 | 0.5876762271 | 0.2716791332 | 0.6100656986 | 0.2404710054 |
| MisraNonSuchIndex | 0.2409829646 | 0.3858529329 | 0.590647161 | 0.2696578205 | 0.6738302112 | 0.25508371 |
| GreenAtmosphericallyResistantVegetationIndex | 0.2192117125 | 0.357783407 | 0.5903590322 | 0.2332133651 | 0.8264268041 | 0.2685987949 |
| TasselledCapNonSuchIndexMSS | 0.2117708176 | 0.3471494615 | 0.5721442103 | 0.222362712 | 0.7997621298 | 0.2150340527 |
| ShapeIndex | 0.0667118281 | 0.1241799071 | 0.4530573785 | 0.0794753954 | 0.2929819226 | -0.1401988715 |
| StructureIntensivePigmentIndex2 | 0.166539371 | 0.2841139734 | 0.5572855473 | 0.1730504632 | 0.8709549904 | 0.1628720015 |
| ChlorophyllIndexRedEdge | 0.1707038134 | 0.2893404663 | 0.5390893817 | 0.1736517698 | 0.9171173573 | 0.1128893569 |
| TCARI_OSAVI | 0.1497377306 | 0.2590892017 | 0.5404892564 | 0.1553403437 | 0.8263528943 | 0.1143891513 |
| MisraSoilBrightnessIndex | 0.1456154138 | 0.2528477907 | 0.536896646 | 0.1496168226 | 0.8342260122 | 0.1007303298 |
| CanopyChlorophyllContentIndex | 0.1538833231 | 0.2649517357 | 0.5632619858 | 0.1554475427 | 0.9697552323 | 0.151463002 |
| StructureIntensivePigmentIndex1 | 0.1525883079 | 0.2636072338 | 0.5584073663 | 0.1551090181 | 0.9698882699 | 0.1397265643 |
| Datt1 | 0.1447619796 | 0.2514667213 | 0.5366957784 | 0.1461048424 | 0.9836086631 | 0.0855116323 |
| MCARI_OSAVI | 0.1359213293 | 0.2378088981 | 0.5239028335 | 0.138000533 | 0.9228879809 | 0.05952923 |
| ChlorophyllVegetationIndex | 0.1365224272 | 0.2387023419 | 0.5263831019 | 0.1377362758 | 0.9743533134 | 0.0773123726 |
| MCARI_OSAVI750 | 0.1277931184 | 0.2251502424 | 0.4960553348 | 0.1300679743 | 0.9091817141 | -0.0033302077 |
| Gitelson2 | 0.1348821372 | 0.2361954004 | 0.5510587096 | 0.135564059 | 0.9902998805 | 0.0898950994 |
| ChlorophyllRedEdge | 0.1292988658 | 0.2273297459 | 0.5041469932 | 0.1294000298 | 0.9951909184 | 0.0025310172 |
| RedEdgeInflectionPoint | 0.1286419034 | 0.2263026685 | 0.4728533924 | 0.1288316548 | 0.990344882 | -0.0137032596 |
| RedEdgePositionLinearInterpolation | 0.1286419034 | 0.2263026685 | 0.4728533924 | 0.1288316548 | 0.990344882 | -0.0137032596 |
| NormG | 0.1291861981 | 0.2271552831 | 0.4547115266 | 0.1291861981 | 1 | -0.0178785715 |
| ColorationIndex | 0.1291861981 | 0.2271552831 | 0.511172533 | 0.1291861981 | 1 | 0.0271825213 |
| ChlorophyllGreen | 0.1291861981 | 0.2271552831 | 0.1650107354 | 0.1291861981 | 1 | -0.0420429446 |
| Intensity | 0.1291861981 | 0.2271552831 | 0.0645930991 | 0.1291861981 | 1 | 0 |
Conclusion
A partir de ces résultats nous pouvons conclure que n'importe quelle combinaison linéaire simple permet d’obtenir des indices de végétation tout aussi performants que les indices définis empiriquement, de plus des modèles plus avancés permettent d'obtenir des résultats plus performant et adaptés aux données récoltées.
Notons également que les indices NDVI = $\frac{n-r}{n+r}$, EnhancedVegetationIndex = $2.5*\frac{n-r}{n+6r-7.5b+1}$, EnhancedVegetationIndex2 = $2.4\frac{n-r}{n+r+1}$ et EnhancedVegetationIndex3 = $2.5\frac{n-r}{n+2.4r+1}$ sont très proche dans leurs formes et propose des performances très différentes après optimisation. On conviendra donc qu'il est plus important d'optimiser la forme de l'équation et les coefficients des bandes spectrales qu'une simple régression, c'est pourquoi nos indices générés automatiquement sont bien plus performants !