Représentation d'un graphe

Article Index

Page 2 of 2

Representation d'un graphe

Il existe plusieurs types de représentation pour décrire un graphe. On distingue principalement la représentation par matrice d'adjacence, par matrice d'incidence sommet-arcs et par liste d'adjacences.

Matrice d'adjacence

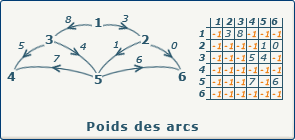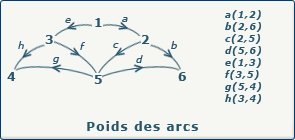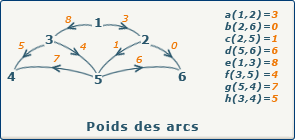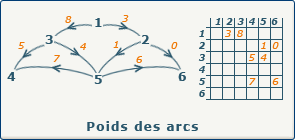
Pour un 1-graphe, la matrice d'adjacence fait correspondre les sommets origines des arcs (classes en ligne dans la matrice) au sommets destination (classes en colonnes dans la matrice). Dans un formalisme matrices booléenne, l'existence d'un arc $(x_{i}, x_{j})$ se traduit par la présence d'un 1 a l'intersection de la ligne $x_{i}$ et de la conne $x_{j}$ et l'absence d'un arc par un 0. Dans un autre formalisme, la valeur correspond a un poid de transition sur l'arc, s'il n'existe pas d'arc, le poid est fixe a $- 1$ . C'est une des représentations les plus utilisées.

donc par exemple on peu simplement utiliser une matrice numpy pour ce type de representation :

n = 4 # number_of_nodes
connection = np.zeros((n,n))
connection[0,0] = 1 # boucle sur x_1
connection[0,2] = 1 # arc de x_1 -> x_3
# etc ....

Matrice d'incidence sommet-arc

Pour établir cette matrice, les lignes sont constituées des sommets du graphe et les connes sont constituées des arcs. On pose la valeur $1$ pour le sommet d'origine et $- 1$ pour le sommet de destination.

encore une fois une simple matrice numpy peu etre utilise, mais ce type de representation est moin flexible a la modification (ajout / suppression d'arc plus couteux)

n = 2 # number_of_nodes
m = 1 # number_of_arcs
connection = np.zeros((n,m))
connection[0,0] = -1 # arc de x_1
connection[1,0] = 1 # vers x_2

Liste d'adjacence

L'objectif ici est de représenter chaque arc par sont extréminée finale, l'extrémintée initial étant défini implicitement. On pose alors que tout les arcs émanant d'un même sommet sont liés entre eux dans une liste. A chaque arc sont associés le sommet de destination et le pointeur au prochain sommet de la liste. Pour un 1-graphe, il y a un avantage à utiliser la représentation par liste d'adjacence grâce à l'application $Γ$ car il y a un gain en place mémoire par rapport à la matrice d'adjacence. Elle est donc mieux adapté pour une implémentation.

La représentation par liste d'adjacence nécéssite la création de deux tableaux. Un premier nommé $L P$ (ListePointeur) de dimension $n + 1$ et un second nommé $L S$ (Liste Successeurs) de dimension $m$ pour les graphes orientés et $2 m$ pour les graphes non-orienté. Pour chaque sommet $i$ , la liste des successeurs de $i$ est contenue dans le tableau $L S$ à partir de la case numéro $L P [i]$ . L'ensemble des informations relatives au sommet $i$ est contenue dans les cases $L P [i]$ à $L P [i + 1] - 1$ du tableau $L S$ .

$w^{+} (i) = L P [i + 1] - L P [i]$ dans le cas orienté
$w^{+} (i) = L P [i + 1] - L P [i]$ dans le cas non-orienté $\to$ identique
$L P [i] = 1 + \sum_{j = 1}^{i - 1} w^{+} (j)$

Cette représentation revient à décrire le graphe par sont application multivoque $i \to Γ (i)$

On construit $L S$ par $Γ (1], Γ (2], . . ., Γ (n]$
On construit $L P$ qui donne pour tout sommet l'indice dans $L S$ ou commence la liste des successeurs.
Pour le sommet $i$ , son premier suivant est $L S [L P [i]]$ et le second $L S [L P [i + 1]]$
L'enssemble ce situe dans les border $L P [i]$ et $L P [i + 1] - 1$ du tableau $L S$
Si un sommet $i$ n'a pas de successeur, on pose $L P [i] = L P [i + 1]$ .
C'est à dire une liste coincée entre les successeurs de $i - 1$ et $i + 1$ .

La place mémoire utilisé est $n^{2}$ pour un graphe d'ordre n. Mais cette fois-ci il existe plusieurs implémentations possibles et on peu ce simplifier un peu la vie en programmation, en utilisant un peu plus de mémoire, c'est a dire en utilisant une liste pour chaque noeud, ce qui simplifie grandement les manipulations et l'ajout/suppression d'arcs :

nodes = [[] for _ in range(nomber_of_nodes)]
nodes[0] = [1] # liste des successeurs de x_1
nodes[1] = [0,2] # liste des successeurs de x_2
nodes[2] = [0,1,4]
nodes[3] = [2]
nodes[4] = [5]
nodes[5] = [2,5] # boucle local

Par contre ce type de représentation ne permet pas de modéliser le poids des arcs, il faut donc rajouter un autres tableau similaire a $L S$ qui en contiendra les poids des arcs. On pourrais également aller plus loin en utilisant des classes.

Voir aussi jerryyin.info