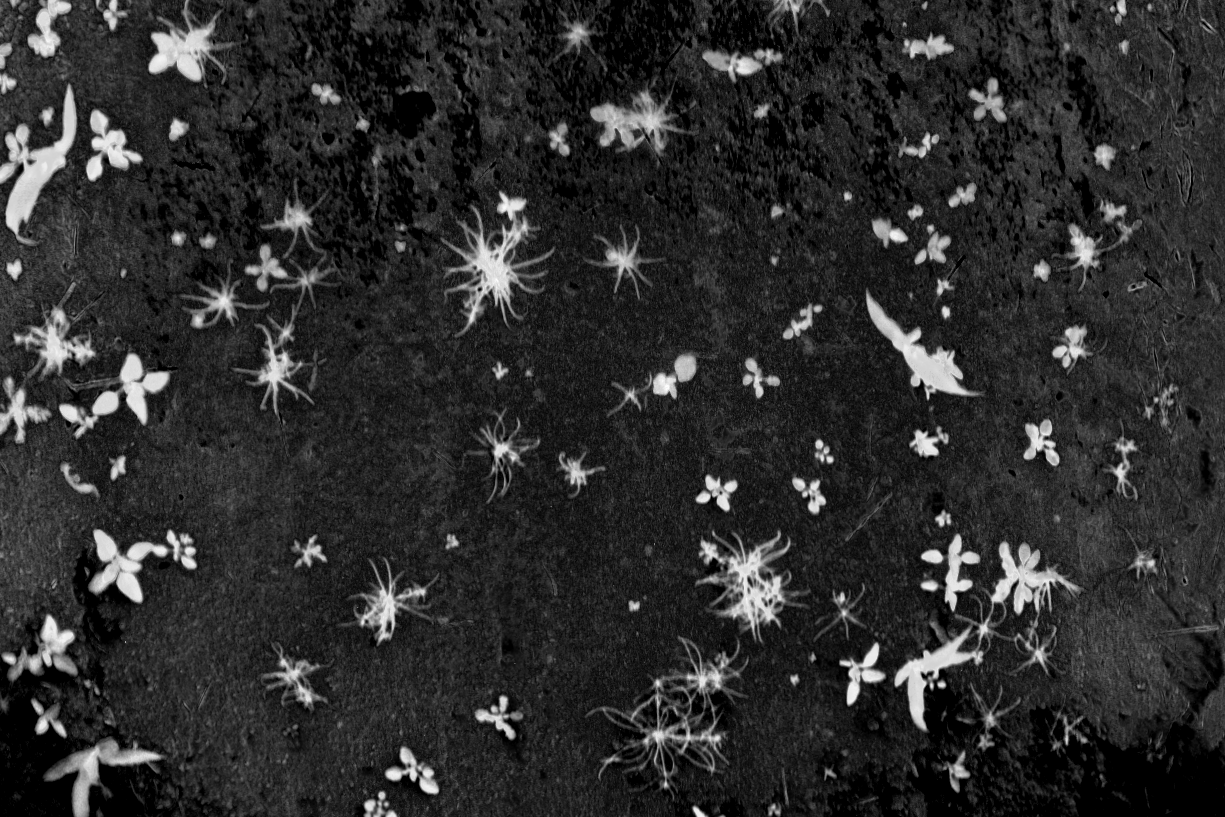
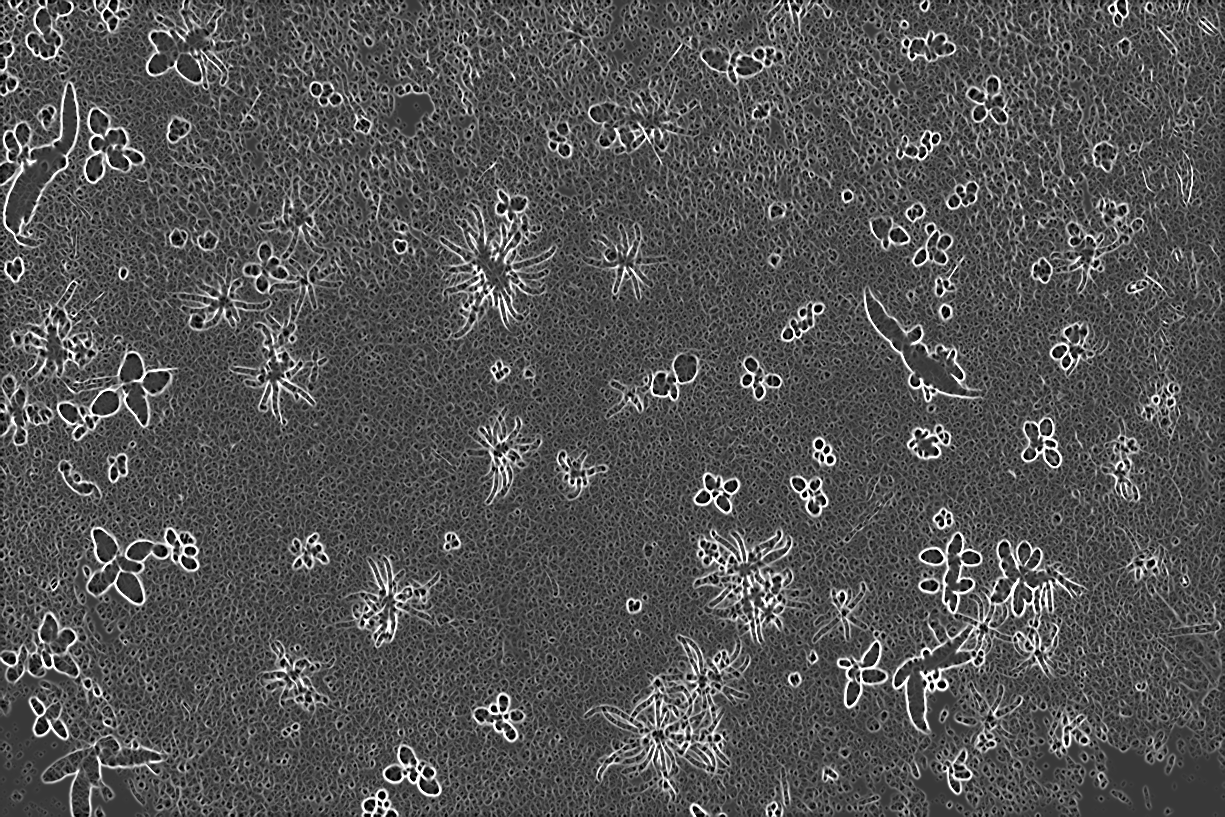
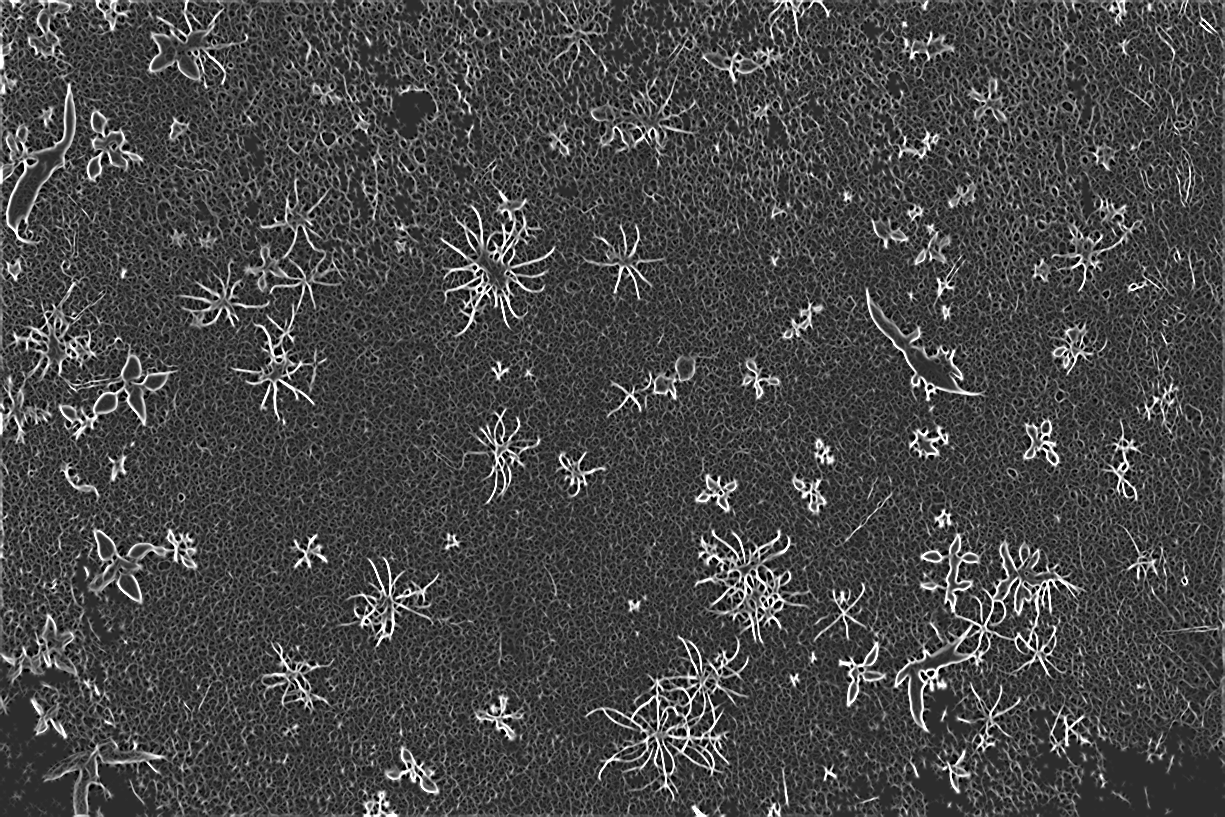
Pré-traitment de l'information
Les bandes spectrales présente par nature un bruit important associer au capteur CCD, ce qui pose des soucis lors de la normalisation. Pour palier à cette effet $1\%$ du signal minimum et maximum est supprimé par le calcul des quantiles, puis chaque bande est normalisée dans l'interval $[0,1]$. Nous ajoutons également quelques transformations des bandes spectrales, afin d'enrichir le pool d'information et de prendre en compte les gradients dans l'image. Le choix s'est orienté vers 5 informations importantes à différents égards :
- L'image de la déviation standard entre toutes les bandes $\lambda_{dev}$
- Le gradient par l'utilisation d'un filtre de Sharr sur $\lambda_{dev}$ noté $\lambda_{grad}$
- Les valeurs propres maximum de la matrice Hessien de $\lambda_{dev}$ noté $\lambda_{ridge_{max}}$
- Les valeurs propres minimales de la matrice Hessien de $\lambda_{dev}$ noté $\lambda_{ridge_{min}}$
- Le laplacien de $\lambda_{dev}$ noté $\lambda_{laplace}$
|
|
|
|
|
|
En effet, ces 5 transformations offrent d'une part une information importante sur le mélange spectral grâce à la déviation standard. Le filtre de Sharr et les valeurs propres maximum donne une information spatiale importante sur la rupture des gradients, donc sur la limite extérieure des objets, ce qui aidera probablement a la convergence. Les valeurs propres minimum, aussi appeler ridge, quant à elle semble détecté facilement les éléments fins tels que les monocotylédones pour des images de végétations.
Indices et forme d’équation
Les indices colorimétriques ont prouvé leur efficacité dans la description des surfaces, ainsi tous les ans différents articles de revue concernant les indices colorimétriques sortent, souvent dans le cadre d'un premier article de thèse appliqué a un domaine d’étude spécifique [Xue Jinru, Çağatay Tanrıverdi, Jiri Mezera]. Nous allons repartir de la base grâce au site www.indexdatabase.de, à partir de cette base de donnée, 89 indices de végétation ont été identifiés comme compatibles avec nos longueurs d'ondes, ils seront ainsi testés. D'autre part, ils seront comparés à nos indices conçus automatiquement. Six formes d'équations simples ont été extraites à partir de l’ensemble des 519 indices de la base de données :
| titre | équation | |
| 1 | une seul bande | $I = \lambda_i$ |
| 2 | soustraction de bande | $I = \lambda_i - \lambda_j$ |
| 3 | différence de 2 bande | $I = \lambda_i / \lambda_j$ |
| 4 | différence normalisé de 2 bande | $I = \frac{\lambda_i - \lambda_j}{\lambda_i + \lambda_j}$ |
| 5 | différence normalisé de 3 bande | $I = \frac{2*\lambda_i - \lambda_j - \lambda_k}{2*\lambda_i + \lambda_j + \lambda_k}$ |
| 6 | différence normalisé "cubique" de 2 bande | $I = \frac{\lambda_i - \lambda_j}{\sqrt{\lambda_i + \lambda_j}}$ |
En analysant ces différentes équations, nous pouvons définir de nouvelles formes d’équation générique qui les synthétisent, et qui prennent en compte l'ensemble des bandes spectrales ainsi qu'un certain voisinage. Deux autres formes d'équations sont également intéressantes à optimiser, qui sont respectivement les approximations de fonction continue par développement de Taylor, ainsi que les approximations de fonction continue par morceaux grâce aux opérateurs morphologiques. Ces équations seront alors optimisées permettant de définir de nouveaux indices automatiquement, dans la seconde partie. L’ensemble de ces méthodes est développé via tensorflow et les paragraphes suivants présente les différents modèles :
Linéaire : Pour synthétiser les équations 1 et 2, nous pouvons définir une simple équation linéaire telle que $I = \sum_{i=0}^{N}{\alpha_i \lambda_i}$. Cette équation peut se généraliser au domaine 2D par une Convolution avec dans sa forme simple une taille de noyaux $k=1,1$.
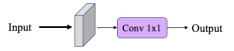
Différence Linéaire : Pour synthétisé les équation 3, 4 et 5, un modèle simple reposant sur une division de deux modèles précédents est possible. De la même façon, cette forme est généralisable au domaine 2D et correspond alors à deux Convolution2D, l'une pour le numérateur, l'autre pour le dénominateur. Nous fixons dans un premier temps la taille des noyaux à $k=1,1$ pour ne pas prendre en considération le voisinage. Nous avons utilisé l'opérateur "nan div"pour remplacer les résultats "not a number" par zero.
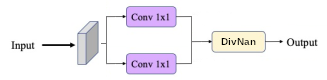
Polynomial : D'après le théorème de Stone–Weierstrass toute fonction continue définie sur un segment peut être approchée uniformément par des fonctions polynomiales. Puisque l'on restreint le segment au domaine $[0-1]$ les polynômes de Bernstein en sont une démonstration commune. Ainsi, toutes forment d'indices colorimétriques peut être approximé par un polynôme $I = \sum_{i=0}^{N}{\alpha_i \lambda_i}^{\delta_i}$. Pour des raisons d'implémentations, deux opérateurs sont défini. D'une part l'exposant $\lambda_i^\delta$, puis l'équation linéaire définie par une Convolution2D pour garder la possibilité de l'étendre au domaine 2D.
Différence Polynomial : En suivant l'idée de la forme précédente et pour respecter la forme d'équations 6, nous introduisons simplement une différence de polynôme, l'un au numérateur permettant d'optimiser la classe recherché et l'autre au dénominateur jouant le rôle de normalisateur $\frac{\sum_{i=0}^{N} \alpha_i \lambda_i ^ {\delta_i} + A} {\sum_{j=0}^{N} \alpha_j \lambda_j ^ {\delta_j} + B}$ ... (voir les réultats si pertinant -> puisque thérème de StoneWeierstrass)
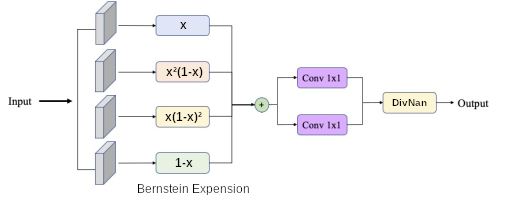
Approximation Universelle de Fonction : En utilisant les développements de Taylor, nous pouvons décomposer n'importe quelle fonction $f(x)$ en $f(x) = f(0) + f'(x) x + \frac{1}{2} f''(x) x^2 + \frac{1}{6} f'''(x) x^3 + o(x^3)$. Une approche pour apprendre cette forme de développement est proposée par [Huang et al., 2017] que l'on appelle communément DenseNet et correspond alors à la somme de la concaténation du signal et de ces dériver $\mathbf{x} \to \left[\mathbf{x}, f_1(\mathbf{x}), f_2(\mathbf{x}, f_1(\mathbf{x})), f_3(\mathbf{x}, f_1(\mathbf{x}), f_2(\mathbf{x}, f_1(\mathbf{x})), \ldots\right]$. Les dérivées sont disponibles par l'utilisation d'une Convolution2D.
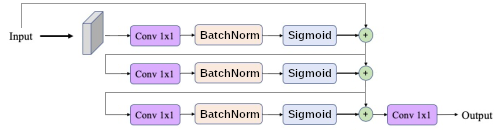https://d2l.ai/chapter_convolutional-modern/densenet.html
Filtre d'entrée : Pour supprimer une partie du signal qui ne serait pas indispensable, nous étudieront l'ajout d'un filtre passe-bande, en amont du réseau. Effectivement, pourquoi prendre en considération l’ensemble des valeurs d'un signal ? Il est très probable que seulement une partie de ce dernier caractérise ce que l'on cherche. Un bon exemple concerne les indices de végétation, seul les valeurs fortes dans le vert et le proche infra-rouge, ainsi que les valeurs faibles dans le rouge et le bleu sont caractéristique de la végétation :
C'est d’ailleurs le principe de l'indice NDVI, en raison des couches spongieuses qui se trouvent sur leur face arrière, les feuilles réfléchissent beaucoup de lumière dans le proche infrarouge, ce qui contraste fortement avec la plupart des objets non-végétaux. Lorsque la plante est déshydratée ou stressée, la couche spongieuse se compresse et les feuilles réfléchissent moins de lumière dans le proche infrarouge, rejoignant les valeurs du rouge, dans le domaine visible. Ainsi, la combinaison mathématique de ces deux signaux peut aider à différencier les plantes des objets non-végétaux et les plantes saines des plantes malades. Cependant cet indice est alors moins intéressant lorsqu'il s’agit de détecter seulement la végétation et est fortement influencé par l’ombrage ou la chaleur.
Nous allons donc ajouter un filtre dans les équations précédentes pour supprimer les valeurs "indésirables" par l'utilisation de deux seuils a et b, qui seront également appris. S'il s’avère que l'ensemble du signal est intéressant, ces deux paramètres ne changeront pas et les valeurs seront a=0 et b=1, dans le cas contraire, a et b changeront. Pour appliquer le premier seuil, on utilise l’équation $y = \max(x-a,0) \div (1-a)$ et permet donc de supprimer les valeurs basses. À partir de ce nouveau signal, on applique l’équation $z = \max(b-y,0) \div b$ pour supprimer les valeurs hautes.
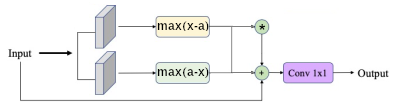
Ces deux paramètres permettent aussi de gérer des paramètre extérieurs, en effet lorsque a devient négatif, le paramètre a pour effet de rehausser le signal, ce dernier est alors compris dans l'intervalle $[a,1]$. Le second paramètre b permet par exemple de supprimer les effets de spéculaires ou de bruit trop important.
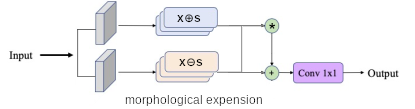
Approximation de fonction par érosion-dilatation : En étendant l'idée de sélection de bandes, nous pouvons non pas en sélectionner une, mais plusieurs, grâce à des opérateurs morphologiques notés $x \oplus s = \max_k(x_k + s_k)$ et $x \ominus s = \max_k(s_k - x_k)$ avec $x_k$ les différentes bandes spectrales et les $s_k$ le coefficient d'érosion de la bande spectrale $\ominus$ ou de dilation $\oplus$. En augmentant le nombre d'érosion dilation, c'est à dire, en définissant plusieurs $s_k$ noté $s_{k,i}$, nous pouvons approximer n'importe quel fonction continue par morceaux [Ranjan Mondal]. Ont pose alors $z_i^{+} = x \oplus s_i = \max_k(x_k + s_{k,i})$ qui est le neurone structurant de dilatation $i$ et $z_i^{-} = x \ominus s_i = \max_k(s_{k,i} - x_k)$ qui est le neurone structurant d'érosion. Pour obtenir la sortie $I = \sum_{i=0}^{N}{z_i^{+}w_i^{+}} + \sum_{i=0}^{N}{z_i^{-}w_i^{-}}$ dont les $w_i^{+}$ et les $w_i^{-}$ sont les coefficients de combinaison linéaire obtenue par Convolution 2D pour rester dans le domaine 2D.
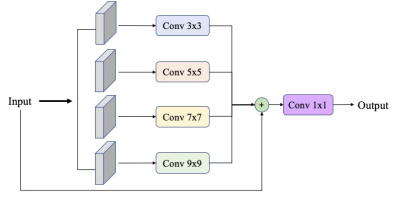
Raffinement spatial de l'indice : Pour prendre en compte différentes échelles dans l'image, nous étudions l'ajout d'une partie en aval du réseau. Appeler "Spatial Pyramide Refinement Block" et consiste en la somme de différentes Convolution2D dont les tailles de noyaux ont été fixé à 1,3,5,7. Le résultat de chaque convolution est concaténé, et le résultat final est donné par une combinaison linéaire de ces différentes échelles modélisées encore une fois par une Convolution2D avec k=1.
Fonction de perte
Dans cette partie, nous présenterons les différentes fonctions de pertes possibles en relation à la classification binaire. Cette partie est inspirée de https://lars76.github.io/neural-networks/object-detection/losses-for-segmentation/. Pour obtenir un indice et faciliter la convergence, on s’intéressera uniquement aux valeurs comprises entre 0 et 1 en sortie de la dernière couche, via une fonction d'activation de type ClippedReLU ($0<=x<=1$), ce qui est négatif ou nul seras donc indésirable et supérieur ou égal à 1 la classe rechercher et entre les deux la frontière d’indécision a optimiser. Les valeurs correspondent alors à la probabilité que le pixel soit la surface rechercher $P(Y=1)=1=p$ ou non $P(Y=0) = 1-p$. Dans ce cas, 4 fonctions sont communément utilisées: Cross-Entropy, Weigthed-Cross-Entropy, Balanced-Cross-Entropy et Focal-Loss (dans la suite nous noterons $p$ la vérité terrain et $\hat{p}$ la prédiction). Dont chacune présentes des intérêts et des limites que nous présentons ci-après :
Cross-Entropy : La cross-entropy peu être défini par $CE(p,\hat{p}) = -p\log(\hat{p}) -(1-p)\log(1-\hat{p})$. C'est une fonction de perte standard qui ne prend pas en compte le ratio des classes (unbalanced). Elle permet de mesurer la séparabilité des classes. Lorsque $CE \rightarrow 0$ il n'y a plus d'entropy et $\hat{p} \rightarrow p$, dans le cas contraire, si $CE \rightarrow 1$ alors $\hat{p}$ et $p$ sont indissociable. La fonction de perte $CE$ ne semble pas être adapté à notre cas, puisque l'on utilise une vérité terrain dont le ratio entre surface rechercher et le reste, des différences pour chaque image.
Weigthed-Cross-Entropy : C'est une variente de $CE$ ou tous les membres de classes positive ($p=1$ sont pondéré par un coefficient $\beta$, lequel permet de réguler le ratio des classe. Ont écris alors $WEC(p,\hat{p}) = -\beta p\log(\hat{p}) -(1-p)\log(1-\hat{p})$. Pour décrémenter l’effet de la classe $Y=0$ ont fixe $\beta>1$ et $\beta<1$ dans le cas contraire. Le coéficient $\beta$ peu être fixé pour maximisé une classe spécifique, ou contrebalancé le ratio des classes. Le coéficient $\beta$ pourrait néanmoins être calcule indépendamment pour chaque image.
Balanced-Cross-Entropy : Cette variente est similaire à WCE, ont introduit cependant $1-\beta$ pour la classe négative. Ont à donc l'équation $BCE(p,\hat{p}) = -\beta p\log(\hat{p}) -(1-\beta)(1-p)\log(1-\hat{p})$. Cette forme est intéressante, puisque $\beta$ peu soit être fixé comme pour $WCE$, soit être calculé pour chaque image, dans ce cas $\beta = \sum(\frac{P(Y=1)}{P(Y=0)})$.
Focal Loss : Cette fonction, proche de BCE essaie décrémenté l'influence des éléments "faciles" pour améliorer en priorité les éléments difficilement séparable. Ont utilise alors deux coefficient $\alpha$ et $\gamma$ sur la distribution de $\hat{p}$. La fonction s'écrit alors $FL(p,\hat{p}) = -(\alpha (1-\hat{p})^\gamma) p\log(\hat{p}) -(1-\alpha)\hat{p}^\gamma(1-p)\log(1-\hat{p})$. La fonction de perte $FL$ ne permet pas de prendre en considération le ratio des classes différents pour chaque image. La fonction ne permet pas d'optimiser l'indice dans l'interval $[0-1]$ avec efficience et donc l'optimisation des métriques définis plus loin. Bien que le coefficient $\alpha$ peu être calculé automatiquement, le coefficient $\gamma$ est difficile à fixé.
Trois autres fonctions de perte sont intéressantes à étudier quand il s'agit de segmentation. Il s'agit de Dice-Loss, TverskyIndex-Loss et IntersectionOverUnion-Loss souvent utilisé dans leurs versions métrique ...
Dice-Loss : La fonction de perte est défini par $ \text{DL}\left(p, \hat{p}\right) = 1 - \frac{2p\hat{p}}{p + \hat{p}}$
IntersectionOverUnion-Loss : Récemment, [Y.Wang et al] ont proposé une solution pour optimisé une approximation de l'intersection sur l'union dans le cas de segmentation binaire. La fonction de perte est défini par $IoU = 1 - \frac{I(p, \hat{p})}{U(p, \hat{p})}$ avec $I(p, \hat{p}) = p\hat{p}$ et $U(p, \hat{p}) = p+\hat{p} - p\hat{p}$. Les performances de cette fonction de perte semble plus éfficiant que les méthodes "simple" précédemment cité [Gell ́ert M ́attyus, Dingfu Zhou, Zhaohui Zheng]
Le choix ce feras donc sur la fonction de perte $BCE$ avec un calcule automatique de $\beta$.
Métrique d’évaluation
Lorsque le nombre d'élément entre chaque classe est fortement déséquilibré, beaucoup de métrique standard sont inéficasse et donc inadapté. Par exemple notre vérité terrain sol/végétation comporte $~83\%$ de sol et donc $~17\%$ de végétation, une mauvaise métrique comme l'accuracy montrera de "bonne" performance. Dans le cas de l'accuracy $\frac{tp+tn}{tp+tn+fp+fn}$ si l'évaluation ne détecte que du sol alors les performances seront de $~83\%$ ce qui n'est donc pas représentatif. Ce que l'on cherche alors est de trouver des métriques permettant de prendre en compte le ratio de chaque classe. Communément les performances des indices colorimétriques est calculé par une cross-entropy $-\frac{1}{N} \sum_{i=0}^{N}{y_{true}\log(y_{pred}) + (1-y_{true})\log(1-y_{pred})}$ entre l'indice et une vérité terrain. Comme nous l'avons vue précédemment cette métrique n'est pas non plus adapté car elle ne prend pas en compte le ratio des classes. Il existe beaucoup d'autres métriques [Abdel Aziz , David Martin Ward Powers, Takaya Saito, László A. Jeni] :
Blanced Accuracy : aussi appelé Youden Statistics pour prendre en compte la ratio des classes, la forme de l'accuracy est transformer afin de calculer séparément les performances de chaque classes et devient donc $\frac{1}{2}(\frac{tp}{tp+fp} + \frac{tn}{tn+fn})$
Dice : Le coefficient de Dice, également appelé indice de recouvremen, est communément utilisé pour vérifier les performances des algorithmes de segmentation $\frac{2p\hat{p}}{p+\hat{p}}$
Mean Intersection Over Union : C'est une autre métrique souvent utiliser pour meusuré les performances de la segmentation, noté $\frac{p\hat{p}}{p+\hat{p} - p\hat{p}}$
Precision : Correspond à une partie de l'équation de balanced accuracy $\frac{tp}{tp+fp}$ et permet de répondre à la question : Quelle proportion des identifications positives a été effectivement correcte ?
Recall : Quelle proportion de vrais positif a été identifiée correctement ? $\frac{tp}{tp+fn}$
Metthews correlation : bla bla bla $\frac{tp*tn - fp*fn}{\sqrt((tp+fp)*(tp+fn)*(tn+fp)*(tn+fn))}$
Comparaison avec les indices standars
Pour effectuer une comparaison juste/equitable il est necessaire d'optimiser chaque indice standar. Pour ce faire un reseaux de neuron minimal est utiliser afin d'apprendre une droite de regression. Le reseaux est donc composé de l'indice spectral, suivit d'une normalisation $x=(x-min)/(min-max)$, puis d'une convolution 2D avec une taille de noyau de $k=1,1$. Puisque l'indice généré une seul dimenssion, l'équation de sortie est alors $I = \alpha * NormalizedIndex + \beta$. Pour effectuer la classification de la meme facons que notre méthode, une activation de type ClipedRelu est utilisé. Evidement les memes métriques et fonction de perte est utilisé.
Reseaux de neurone simple
| AdventicedTransformedSoilAdjustedVI AnthocyaninRefectanceIndex AshburnVegetationIndex AtmosphericallyResistantVegetationIndex2 AtmosphericallyResistantVegetationIndex AverageReflectance750to850 BlueWideDynamicRangeVegetationIndex BrowningReflectanceIndex CanopyChlorophyllContentIndex ChlorophyllAbsorptionRatioIndex2 ChlorophyllAbsorptionRatioIndex ChlorophyllGreen ChlorophyllIndexGreen ChlorophyllIndexRedEdge710 ChlorophyllIndexRedEdge ChlorophyllRedEdge ChlorophyllVegetationIndex ColorationIndex CorrectedTransformedVegetationIndex CRI700 Datt1 Datt4 Datt6 DifferencedVegetationIndexMSS DifferenceNIRGreenVegetationIndex DoubleDifferenceIndex EnhancedVegetationIndex2 EnhancedVegetationIndex3 EnhancedVegetationIndex Gitelson2 |
GlobalEnvironmentMonitoringIndex |
NormNir |