Comparaison k-ppv et bayes

• Séparez nos données en sous-ensembles disjoints (apprentissage et test) :
  • Ont utilise la syntaxe data[0:80] et data[80:100] pour avoir deux ensembles disjoints
  • les 80 premiers et les 20 derniers tout simplement ... car il y a 100 éléments donc 20-80%
• Mettre en place l’algorithme des lois normales et la méthode de K-ppv
  • Ont repdnre les exercices précédent quel l'on applique à de nouvelles données
  • calculé sur deux sous-ensembles disjoints (apprentissage / tests).
• Évaluez vos systèmes : matrice de confusion, un taux de reconnaissance ...

Évaluation

Voici les résultats trouvés avec K = 3 pour kppv (à gauche) et avec la loi normal (à droite)

Quels sont avantages/inconvénients des deux méthodes ?

A ce stade on ne peut pas conclure sur la qualité de la classification. Malgré une meilleure reconnaissance de la classe 8 avec l’algorithme des k-ppv, il faudrait beaucoup plus de jeux de tests, les deux algorithmes ont le même taux de reconnaissance, en revanche le temps d’exécution est bien meilleur pour la loi normale. Personnellement je prendrais l’algorithme de la loi normale en ajoutant des critères de sélection pour augmenter le taux de reconnaissance cela nous permettrait d’avoir un plus grand contrôle sur la classification avec de meilleurs temps de calcul voir même de les paralléliser. Nous pouvons par contre extraire les informations suivantes :

Variations du nombre de points en apprentissage et en test.

On remarque que la loi normale est plus efficace lorsque l’on passe de 20 à 30 points (les premiers) en fait on a un meilleur taux de reconnaissance puisqu’il y a une plus grande couverture de données appartenant à la zone de recouvrement par rapport à la densité de probabilité d’une loi gaussienne. Réciproquement, lorsqu’il n’y a plus suffisamment de point représentant l’information dans les données d’apprentissage le taux de reconnaissance diminue (à la fin) → normale.

L’algorithme des k-ppv suit à peu près la même logique avec des taux de reconnaissance légèrement inférieurs à celui de la loi normale. Ce qui peut peut-être s'expliquer par le fait que quand il y a plus de points en apprentissage des erreurs peuvent se produire si ces points sont des extremums de classe. Que l’on voie en cross-validation (dans l’intervalle 20-40)

Validation croisée / cross-validation

Le principe c'est qu'on change l'intervalle des points qu'on sélectionne pour les données en apprentissage et en test. On fait simplement un décalage de la fenêtre des jeux de test. Ci-dessous, les résultats que j'ai obtenu avec une fenêtre de taille 20 avec un pas de 1 puisque les données suivent une loi gaussienne il est normale que le taux de reconnaissance soit plus faible sur les bords. De plus on pourrais ajuster l’algorithme au données avec la superposition de deux lois normales par classe.

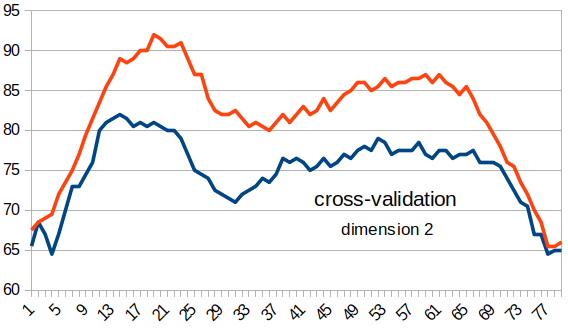
On conclu que la loi normale est plus efficace que le kppv lorsqu'on effectue la cross-validation. Bien que encore une fois il faudrait d’avantage de jeux de tests pour conclure sur les résultats dans une démarche scientifique optimale.

Puisque le programme n’est pas optimisé, par exemple avec sse et que l’algorithme des kppv utilise beaucoup de calculs de distances, le temps d’exécution explose rapidement heureusement que les tests n'ont pas beaucoup d’éléments.

Encore une fois malgré le fait que l’algorithme des kppv a un meilleur taux de reconnaissance, je prendrais la loi normale qui donne tout de même un bon taux de reconnaissance a partir de 25 % de données d’apprentissage mais permet de traiter beaucoup plus rapidement l’information.

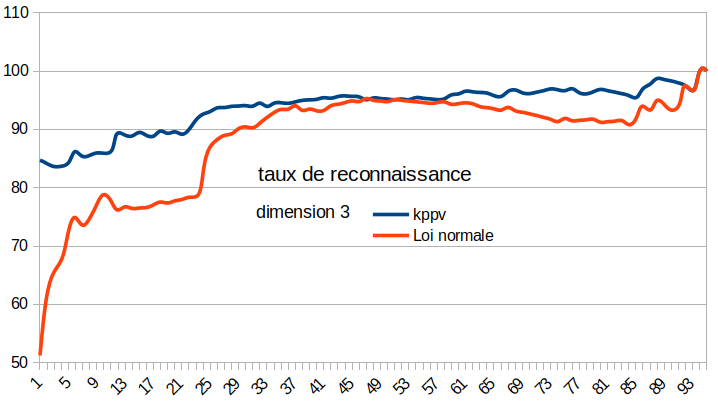
 On remarque que le taux de reconnaissance est largement supérieur quand on augmente le nombre de dimensions, mais encore une fois, il faudrait d’avantage de données à tester pour garantir les observations que l’on fait présentement.

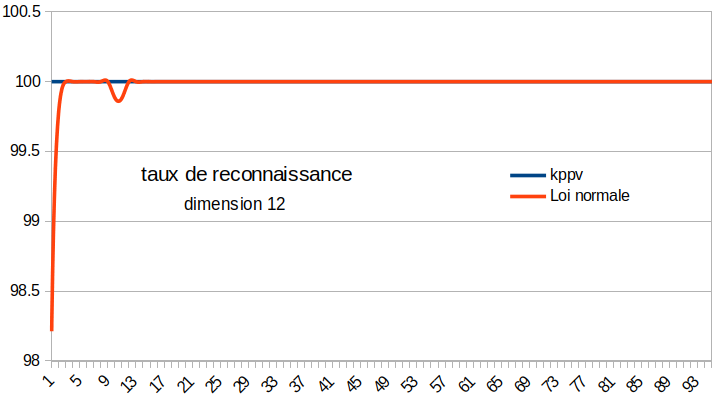
On remarque que le temps d'exécution pour le kppv en dimension 12 est presque multiplié par deux tandis que la loi normale est en fait assez constante. Encore une fois je prendrais l’algorithme de la loi normale qui donne quasiment le même taux de reconnaissance à partir de 13% de données d’apprentissage mais permet de traiter beaucoup plus rapidement l’information.