Recherche dichotomique

En informatique, rechercher un élément dans un tableau est un problème récurrent et parfois coûteux. Nous allons voir ici une méthode simple permettant de trouver un élément dans un tableau trié et grâce à cette propriété nous allons voir comment diminuer drastiquement le nombre d'itérations nécessaires. La recherche dichotomique, également connue sous le nom de recherche binaire, est une technique algorithmique utilisée pour trouver la position d'une valeur cible dans une liste ou un tableau trié. L'idée de base de la recherche dichotomique est de diviser la liste en deux de manière répétée et d'écarter la moitié des éléments restants en les comparant à la valeur cible, jusqu'à ce que cette dernière soit trouvée ou que la liste soit épuisée. On peut donc écrire cette première propriété :

• (1) $\forall i, j \in [0, N] \mid i < j \land T[i] < T[j] \Rightarrow \text{triée}$

La recherche dichotomique consiste à diviser l'espace de recherche (valeur = valeur recherchée). En effet, il en résulte que, grâce à la propriété (1) si T[i]<valeur alors la propriété (1) induit une nouvelle propriété (2). Il en résulte également que si $T[x]>valeur$ alors la propriété (1) induit la propriété (3). Que l'on peut réécrire :

• (2) ${ \forall y \in [0..x],\ T[y] < \text{valeur} \land \exists w \in (x..N] \mid T[w] = \text{valeur} }$
  • La valeur se trouve dans le sous-ensemble de gauche
• (3) ${ \forall y \in [x..N],\ T[y] > \text{valeur} \land \exists w \in [0..x) \mid T[w] = \text{valeur} }$
  • La valeur se trouve dans le sous-ensemble de droite

En excluant une des deux parties à chaque itération, le nouvel ensemble est soumis à la même propriété (1) qui induit (2) et (3). L'algorithme prend, si possible, le milieu comme point de comparaison ($T[x]$) pour exclure la partie la plus grande possible à chaque itération ($N/2+1$), on peut extraire les sous-propriétés (4) et (5) du nouvel ensemble :

• (4) ${ \exists w \in [0..N] \mid T[w] = \text{valeur} }$
  • La valeur existe dans l'intervalle
• (5) ${ |U| < |E| }$
  • La taille du sous-ensemble diminue

Finalement, le tableau est vu comme un arbre de recherche où chaque itération élimine une branche droite ou gauche et son sommet :

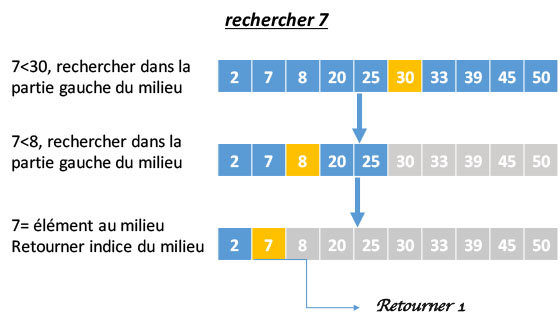
La complexité temporelle de la recherche dichotomique est $O(\log n)$, où n est le nombre d'éléments de la liste ou du tableau trié. Elle est donc beaucoup plus rapide que la recherche linéaire, dont la complexité temporelle est de $O(n)$. La recherche dichotomique est largement utilisée en informatique et en ingénierie pour diverses applications, telles que la recherche d'une valeur dans une base de données, les algorithmes de tri et la recherche de racines d'équations en analyse numérique.

Implémentation

template<class T>
inline long dichotomicsearch(const T* array, size_t size, T val) noexcept
{
    size_t start = 0, end = size-1;
    size_t mid = (start+end)/2;

    // the input array must be sorted
    assert(std::is_sorted(array, array+size)); // (1)

    if(array[0] == val)
        return 0;
    // exclude [0] and [end] for performance & assertion test
    if(array[size-1] == val)
        return size-1;

    while(start <= end && array[mid] != val)
    {
        long diff = val-array[mid];
        bool iv = (diff < 0)*(~0); // 1111..1111 si diff<0 sinon 0000.0000
        bool ni = ~iv;              // 0000..0000 si diff>=0 sinon 1111..1111

        // the new subset is reduced on each iteration until the element is found
        // otherwise the size of the subset become negative, so the element isn’t on the list (exit)
        assert((iv&(mid+1)) + (start&ni) + (ni&(mid-1)) + (end&iv) < start+end); // (5)

        start = (iv&(mid+1)) | (start&ni); //<= if(diff < 0) start = mid+1
        end = (ni&(mid-1)) | (end&iv);     //<= if(diff >= 0) end = mid-1;
        mid = (start+end)/2;

        // each excluded subset does not contain @val
        // by equivalence this assertion this equals to say:
        //       all element of the left subset doesn't contain @val
        //       and the subset is sorted so max(left)<@val & min(right)>@val
        // idem for the right subset

        assert(*std::max_element(array, array+start) < val); // (2)
        assert(*std::min_element(array+end, array+size-1) > val); // (3)
        // so val is on the subspace [start-end]
        assert(std::binary_search(array+start, array+end, val) != -1); // (4)
    }

    return array[mid] == val ? mid : -1;
}