Objectifs du TP
- Comprendre les limites du perceptron simple et la nécessité des réseaux multicouches
- Implémenter l’algorithme de rétropropagation du gradient
- Analyser l’impact de l’architecture du réseau sur les performances
- Appliquer les réseaux multicouches à des problèmes non-linéairement séparables
- Étudier les phénomènes de sur-apprentissage et de sous-apprentissage
Livrables Attendus
Code
- Implémentation complète de la classe
PerceptronMultiCouches - Implémentation de la classe
CoucheNeurones - Scripts de test et de visualisation avancés
- Comparaisons avec le perceptron simple
- Completer le rapport précédent
Rapport
- Introduction : Du perceptron simple au réseau multicouches
- Méthodes :
- Architecture des réseaux multicouches
- Algorithme de rétropropagation
- Fonctions de coût et d’optimisation
- Résultats :
- Résolution du problème XOR
- Tests sur datasets synthétiques et réels
- Analyse de l’impact de l’architecture
- Courbes d’apprentissage et de validation
- Discussion :
- Avantages et inconvénients des réseaux multicouches
- Problèmes de sur-apprentissage
- Stratégies de régularisation
- Conclusion : Bilan et perspectives
Visualisations
- Surfaces de décision en 2D
- Courbes d’apprentissage (loss et accuracy)
- Visualisation des poids appris
- Comparaisons de performances selon l’architecture
- Analyse du sur-apprentissage
Notation
Démarche similaire au TP précédent :
| Critère | Points |
|---|---|
| Implémentation du code | (7 points) |
| -------------------------------------------------- | -------- |
| PerceptronMultiCouches | 2 |
| CoucheNeurones | 3 |
| Test et validation sur dataset | 2 |
| -------------------------------------------------- | -------- |
| Rapport écrit et analyse | (13 points) |
| -------------------------------------------------- | -------- |
| Introduction (enjeux, transition MLP) | 1 |
| Méthodes : architecture, rétropropagation, coût | 2 |
| Résultats : | |
| > Résolution XOR, jeux synthétiques et réels, impact architecture (largeur, profondeur) | 3 |
| > Courbes d’apprentissage (loss, accuracy, val_loss) | 1 |
| Discussion : analyse critique, réponses aux questions, sur/sous-apprentissage, régularisation | 5 |
| Conclusion : bilan, perspectives, limites | 1 |
Partie 1 : Limites du Perceptron et introduction aux réseaux multicouches
1.1 Rappel des limitations du perceptron simple
Comme nous l’avons vu dans le TP précédent, le perceptron simple ne peut résoudre que des problèmes linéairement séparables. Cette limitation fondamentale a été formalisée en 1969 par Marvin Minsky et Seymour Papert dans leur ouvrage “Perceptrons”, qui a montré mathématiquement que certains problèmes simples, comme la fonction XOR (vue précédement), sont impossibles à résoudre avec un seul neurone.
Cette découverte a provoqué le premier “hiver de l’intelligence artificielle”, car elle semblait condamner les réseaux de neurones à ne traiter que des problèmes triviaux. Il a fallu attendre les années 1980 et la redécouverte de l’algorithme de rétropropagation pour relancer l’intérêt pour les réseaux de neurones.
1.2 L’architecture multicouche comme solution
La solution à ce problème consiste à empiler plusieurs couches de neurones, créant ainsi ce qu’on appelle un Multi-Layer Perceptron (MLP). L’idée fondamentale est que les couches intermédiaires (appelées couches cachées) peuvent apprendre des représentations internes des données, transformant l’espace d’entrée de manière à rendre les classes linéairement séparables dans cet nouvel espace. C’est une projection dans un espace latent.
Architecture typique d'un réseau multicouches (Miguel Pérez-Enciso 2019)
L’idée semble simple : si une couche ne suffit pas, ajoutons-en deux, trois… Un réseau multicouches se compose de :
- Couche d’entrée : reçoit les données brutes (en vert)
- Couches cachées : transforment progressivement la représentation des données (bleu)
- Couche de sortie : produit la prédiction finale (rouge)
Mais dans la pratique, l’apprentissage d’un réseau à plusieurs couches s’est longtemps heurté à des obstacles majeurs. Dès les années 1960-70, des chercheurs tentent de construire des réseaux de neurones comportant plus d’une couche cachée. Ces tentatives montrent des résultats prometteurs, mais sont extrêmement instables :
- Les fonctions d’activation utilisées, comme la Heaviside, ne sont pas différentiables, rendant l’apprentissage par gradient impossible.
- Même avec des fonctions différentiables (comme sigmoïde ou tanh), le calcul des dérivées dans les couches intermédiaires est mal compris ou approximé, menant à des mises à jour erronées.
- En l’absence d’un algorithme général, chaque nouvelle architecture nécessite un algorithme spécifique.
Cela limite les réseaux à deux voire trois couches maximum, souvent avec un entraînement manuel ou par tâtonnement. Au fil des années, certaines équipes expérimentent des MLP comportant jusqu’à 4 ou même 8 couches, dans l’espoir d’augmenter leur capacité de représentation. Mais ces modèles souffrent :
- De convergence lente ou absente.
- D’une instabilité numérique (poids explosifs ou nulles).
- Du problème du gradient qui disparaît (surtout avec des sigmoïdes sur plusieurs couches).
Faute de méthode stable et généralisable, ces architectures sont rarement utilisées à grande échelle. Tout change en 1986, avec les travaux fondateurs de David Rumelhart, Geoffrey Hinton et Ronald Williams, qui introduisent une méthode rigoureuse de propagation du gradient à travers un réseau de n’importe quelle profondeur : la backpropagation. Le principe est le suivant :
- Propagation avant (forward pass) : on calcule la sortie du réseau couche par couche.
- Calcul de l’erreur de sortie : comparaison avec la sortie attendue.
- Propagation arrière (backward pass) : on propage l’erreur à l’envers, en utilisant la dérivée des fonctions d’activation pour chaque couche.
- Mise à jour des poids : les poids sont ajustés par descente du gradient.
C’est senssiblement la démarche que nous avons commencé à mettre en place dans le TP précédent.
1.3 Théorème d’approximation universelle
Le théorème d’approximation universelle, démontré par George Cybenko en 1989 (pour les fonctions d’activation sigmoïdes) puis généralisé à d’autres fonctions par Kurt Hornik, établit un résultat fondamental :
Un réseau de neurones avec une seule couche cachée contenant un nombre fini mais suffisant de neurones peut approximer n’importe quelle fonction continue sur un domaine compact de ℝⁿ, avec une précision arbitraire.
Autrement dit, les réseaux de neurones sont des approximateurs universels. Ce résultat est à la base du succès des MLP : bien qu’un seul neurone ne puisse modéliser qu’un seuil, une somme pondérée de neurones non-linéaires peut approcher des fonctions beaucoup plus riches et complexes. Il existe d’autres architectures de réseaux de neurones qui permettent d’approximer des fonctions non continues, etc. Par exemple les berstein neural network.
Dans un réseau de neurones avec une couche cachée, l’approximation d’une fonction $f$ s’écrit sous la forme :
$$
f(x) \approx \sum_{i=1}^{N} \alpha_i \cdot \sigma(w_i^T x + b_i)
$$
où :
- $\sigma$ est la fonction d’activation (ex : sigmoïde, ReLU…),
- $w_i$ et $b_i$ sont les poids et biais des neurones de la couche cachée,
- $\alpha_i$ sont les poids de la couche de sortie.
Théorème de Taylor
Ce phénomène d’approximation évoque fortement le développement en série bien connu en mathématiques. Rappelons qu’une fonction lisse peut être approximée localement par un polynôme de Taylor, c’est-à-dire une somme pondérée de dérivées successives autour d’un point :
$$
f(x) \approx \sum_{k=0}^n \frac{f^{(k)}(x_0)}{k!}(x - x_0)^k
$$
C’est une somme pondérée des puissances de $(x - x_0)$, avec les poids donnés par les dérivées successives. On remarque une structure analogue : c’est une somme pondérée de fonctions non linéaires paramétrées. Comme pour le développement de Taylor, plus on augmente le nombre de termes (ici, de neurones), plus l’approximation peut être précise.
Dans un réseau de neurones, la profondeur du réseau (le nombre de couches) pourrait être vue comme une analogie du degré $k$ du polynôme de Taylor, représentant le raffinement progressif de l’approximation.
Intégrale de Riemann
Une autre analogie utile est celle de l’intégrale de Riemann : pour approximer l’aire sous une courbe, on la découpe en une somme finie de rectangles. Plus on augmente le nombre de rectangles (et donc réduit leur largeur), plus l’approximation devient précise. L’intégrale de Riemann d’une fonction $f$ sur l’intervalle $[a, b]$ est donnée par :
$$
\int_a^b f(x) \, dx \approx \sum_{i=1}^N f(x_i^*) \, \Delta x
$$
où chaque $x_i^*$ est un point dans le sous-intervalle $[x_{i-1}, x_i]$ et $\Delta x = \frac{b - a}{N}$ est la largeur des intervalles. Plus on augmente $N$, plus l’approximation devient précise. De manière similaire, un réseau de neurones approxime une fonction continue en la décomposant en une somme finie de fonctions simples (Heaviside ce rapprochant du rectangle), les activations pondérées des neurones. Chaque neurone agit un peu comme un “rectangle” (forme dependent de la fonction d’activation) dans l’intégrale de Riemann : grossier au début, mais qui affine l’approximation en se multipliant.
Dans cette analogie, la largeur du réseau (le nombre de neurones dans la couche cachée) pourrait être associée au nombre $N$ de subdivisions dans l’intégrale de Riemann : plus il est élevé, plus l’approximation est fine.
Exercice 1.1 - Questions d’analyse théorique :
- Que signifie concrètement le théorème d’approximation universelle ?
- Ce théorème garantit-il qu’on peut toujours trouver les bons poids ?
- Quelle est la différence entre “pouvoir approximer” et “pouvoir apprendre” ?
- Pourquoi utilise-t-on souvent beaucoup plus de couches cachées en pratique ?
- En principe, vous avez déjà vu au lycée un autre type d’approximateur de fonctions, donner leurs noms ?
Exercice 1.2 - Expliquer la phrase suivante
Le théorème d’approximation universelle affirme qu’un réseau profond peut exactement retrouver les données d’entraînement.
Partie 2 : Propagation avant
2.1 Formalisation mathématique
Dans un réseau multicouches, l’information se propage de couche en couche selon le processus suivant. Pour une couche $l$ avec $n^{(l)}$ neurones recevant les sorties $a^{(l-1)}$ de la couche précédente :
- Combinaison linéaire : $z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)}$
- Activation : $a^{(l)} = f^{(l)}(z^{(l)})$
où :
- $W^{(l)}$ est la matrice des poids de dimension $(n^{(l)}, n^{(l-1)})$
- $b^{(l)}$ est le vecteur des biais de dimension $(n^{(l)}, 1)$
- $f^{(l)}$ est la fonction d’activation de la couche $l$
Cette passe reste similaire au TP précédent, ici nous avons simplement une ecriture matriciel.
2.2 Implémentation d’une couche de neurones
Exercice 2.2.1 :
Implémentez la partie forward de la classe représentant une couche de neurones, ci-dessous. Vous devez développer un test unitaire afin de valider le bon fonctionnement de la méthode forward.
import numpy as np
class CoucheNeurones:
def __init__(self, n_input, n_neurons, activation='sigmoid', learning_rate=0.01):
"""
Initialise une couche de neurones
Parameters:
- n_input: nombre d'entrées
- n_neurons: nombre de neurones dans cette couche
- activation: fonction d'activation ('sigmoid', 'tanh', 'relu')
- learning_rate: taux d'apprentissage
"""
self.n_input = n_input
self.n_neurons = n_neurons
self.activation_name = activation
self.learning_rate = learning_rate
# Initialisation Xavier/Glorot pour éviter l'explosion/disparition des gradients
limit = np.sqrt(6 / (n_input + n_neurons))
self.weights = np.random.uniform(-limit, limit, (n_neurons, n_input))
self.bias = np.zeros((n_neurons, 1))
# Variables pour stocker les valeurs lors de la propagation
self.last_input = None
self.last_z = None
self.last_activation = None
# Import de la fonction d'activation du TP précédent
from activation_functions import ActivationFunction
self.activation_func = ActivationFunction(activation)
def forward(self, X):
"""
Propagation avant
X: matrice d'entrée (n_features, n_samples)
"""
# TODO: Implémenter la propagation avant
# Stocker les valeurs intermédiaires pour la rétropropagation
self.last_input = X
self.last_z = 0 # Combinaison linéaire
self.last_activation = 0 # Après fonction d'activation
return self.last_activation
def backward(self, gradient_from_next_layer):
"""
Rétropropagation
gradient_from_next_layer: gradient venant de la couche suivante
"""
# TODO: Calculer les gradients par rapport aux poids et biais
# TODO: Calculer le gradient à propager vers la couche précédente
# Gradient par rapport à la fonction d'activation
grad_activation = 0
# Gradient par rapport aux poids
grad_weights = 0
# Gradient par rapport aux biais
grad_bias = 0
# Gradient à propager vers la couche précédente
grad_input = 0
# Mise à jour des paramètres
self.weights -= self.learning_rate * grad_weights
self.bias -= self.learning_rate * grad_bias
return grad_input
2.3 Implémentation du réseau
Exercice 2.2.2 :
Créez la partie forward de la classe principale pour le perceptron multicouches, ci-dessous. Vous devez développer un test unitaire afin de valider le bon fonctionnement de la méthode forward.
class PerceptronMultiCouches:
def __init__(self, architecture, learning_rate=0.01, activation='sigmoid'):
"""
architecture: liste des tailles de couches [input_size, hidden1, hidden2, ..., output_size]
"""
self.architecture = architecture
self.learning_rate = learning_rate
self.activation = activation
self.couches = []
self.history = {'loss': [], 'val_loss': [], 'accuracy': [], 'val_accuracy': []}
# Création des couches
for i in range(len(architecture) - 1):
# TODO: Créer les couches successives
# La dernière couche peut avoir une activation différente
activation_couche = activation
if i == len(architecture) - 2: # Dernière couche
activation_couche = 'sigmoid' # ou 'softmax' pour multi-classes
couche = CoucheNeurones(
n_input=architecture[i],
n_neurons=architecture[i+1],
activation=activation_couche,
learning_rate=learning_rate
)
self.couches.append(couche)
def forward(self, X):
"""
Propagation avant à travers tout le réseau
"""
current_input = X.T # Transposer pour avoir (n_features, n_samples)
# TODO: Propager les données à travers toutes les couches
return current_input.T # Retransposer pour avoir (n_samples, n_output)
def backward(self, X, y_true, y_pred):
"""
Rétropropagation à travers tout le réseau
"""
# TODO: Calculer le gradient initial (dérivée de la fonction de coût)
# Pour l'erreur quadratique : gradient = (y_pred - y_true)
# TODO: Propager le gradient vers l'arrière
def train_epoch(self, X, y):
"""
Une époque d'entraînement
"""
# Propagation avant
y_pred = self.forward(X)
# Calcul de la fonction de perte
loss = self.compute_loss(y, y_pred)
# Rétropropagation
self.backward(X, y, y_pred)
return loss, y_pred
def compute_loss(self, y_true, y_pred):
"""
Calcule la fonction de coût (erreur quadratique moyenne)
"""
# TODO: Implémenter l'erreur quadratique moyenne
return 0
def fit(self, X, y, X_val=None, y_val=None, epochs=100, verbose=True):
"""
Entraîne le réseau
"""
for epoch in range(epochs):
# Entraînement
loss, y_pred = self.train_epoch(X, y)
accuracy = self.compute_accuracy(y, y_pred)
self.history['loss'].append(loss)
self.history['accuracy'].append(accuracy)
# Validation si données fournies
if X_val is not None and y_val is not None:
y_val_pred = self.predict(X_val)
val_loss = self.compute_loss(y_val, y_val_pred)
val_accuracy = self.compute_accuracy(y_val, y_val_pred)
self.history['val_loss'].append(val_loss)
self.history['val_accuracy'].append(val_accuracy)
if verbose and epoch % 10 == 0:
print(f"Époque {epoch:3d} - Loss: {loss:.4f} - Acc: {accuracy:.4f}")
def predict(self, X):
"""
Prédiction sur de nouvelles données
"""
return self.forward(X)
def compute_accuracy(self, y_true, y_pred):
"""
Calcule l'accuracy pour la classification binaire
"""
# TODO: Implémenter le calcul d'accuracy
# Pour la classification binaire : seuil à 0.5
predictions = (y_pred > 0.5).astype(int)
return np.mean(predictions.flatten() == y_true.flatten())
Partie 3 : Rétropropagation
L’algorithme de rétropropagation (backpropagation) est au cœur de l’entraînement des réseaux multicouches. Il s’agit d’une application élégante de la règle de dérivation en chaîne pour calculer efficacement les gradients de la fonction de coût par rapport à tous les paramètres du réseau.
Le processus se déroule en plusieurs phases :
- Initialisation des poids et biais
- Propagation avant (forward pass) : calcul de la sortie du réseau couche par couche (avec sauvegarde)
- Calcul des erreurs en partant de la sortie
- Rétropropagation (backward pass) : propagation de l’erreur de la sortie vers l’entrée
Dit autrement l’algorithme de rétropropagation peut être compris comme un processus de “retour d’information” où le réseau apprend de ses erreurs . Contrairement à l’intuition, ce n’est pas magique : c’est une application systématique du calcul différentiel pour déterminer comment chaque paramètre influence l’erreur finale.
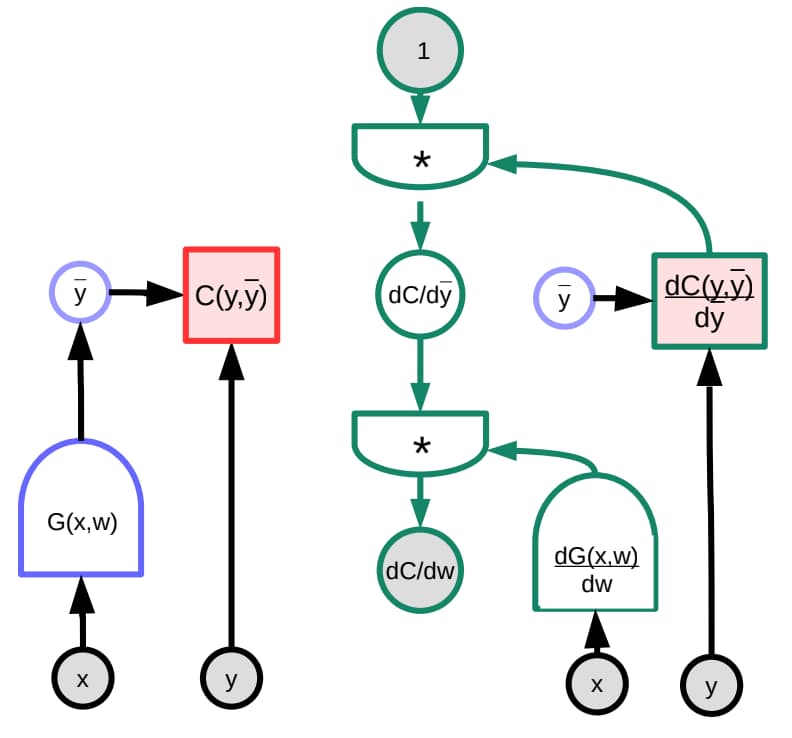
Illustration graphique de la rétropropagation (Loïck Bourdois 2020)
Avant de plonger dans les calculs, clarifions nos notations :
- $L$ : fonction de coût (loss)
- $W^{(l)}$ : matrice des poids de la couche $l$
- $b^{(l)}$ : vecteur des biais de la couche $l$
- $z^{(l)}$ : entrées pré-activation de la couche $l$
- $a^{(l)}$ : sorties (activations) de la couche $l$
- $f^{(l)}$ : fonction d’activation de la couche $l$
- $\delta^{(l)}$ : “erreur” de la couche $l$ (gradient de $L$ par rapport à $z^{(l)}$)
3.1 Règle de dérivation en chaîne
Si nous avons une fonction composée $f(g(x))$, alors :
$$\frac{df}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}$$
Dans un réseau multicouches, la fonction de coût $L$ (pour loss) dépend des paramètres de toutes les couches. Pour une couche $l$, le gradient s’écrit :
$$\frac{\partial L}{\partial W^{(l)}} = \frac{\partial L}{\partial z^{(l)}} \cdot \frac{\partial z^{(l)}}{\partial W^{(l)}}$$
3.2 Dérivation des équations de rétropropagation
Pour la couche de sortie :
Le gradient par rapport aux activations de sortie :
$$\delta^{(L)} = \frac{\partial L}{\partial z^{(L)}} = \frac{\partial L}{\partial a^{(L)}} \odot f’^{(L)}(z^{(L)})$$
Pour les couches cachées :
$$\delta^{(l)} = ((W^{(l+1)})^T \delta^{(l+1)}) \odot f’^{(l)}(z^{(l)})$$
Gradients des paramètres :
$$\frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (a^{(l-1)})^T$$
$$\frac{\partial L}{\partial b^{(l)}} = \delta^{(l)}$$
où $\odot$ représente le produit élément par élément (Hadamard).
Synthèse des équations utiles :
| Étape | Formule | Description |
|---|---|---|
| Calcul de l’erreur | $\delta = \frac{\partial L}{\partial a^{(L)}} \odot f’(z^{(L)})$ | Erreur de la couche de sortie |
| Delta couche sortie | $\delta^{(L)} = (a^{(L)} - y) \odot f’(z^{(L)})$ | Delta (erreur) de la couche de sortie |
| Gradient poids sortie | $\frac{\partial L}{\partial W^{(L)}} = \delta^{(L)} (a^{(L-1)})^T$ | Gradient des poids de sortie |
| Gradient biais sortie | $\frac{\partial L}{\partial b^{(L)}} = \delta^{(L)}$ | Gradient des biais de sortie |
| Delta couche cachée | $\delta^{(l)} = \left((W^{(l+1)})^T \delta^{(l+1)}\right) \odot f’(z^{(l)})$ | Delta des couches cachées (propagation arrière) |
| Gradient poids cachés | $\frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (a^{(l-1)})^T$ | Gradient des poids des couches cachées |
| Gradient biais cachés | $\frac{\partial L}{\partial b^{(l)}} = \delta^{(l)}$ | Gradient des biais des couches cachées |
| Mise à jour poids | $W^{(l)} \leftarrow W^{(l)} - \eta \frac{\partial L}{\partial W^{(l)}}$ | Mise à jour des poids ($\eta$ = taux d’apprentissage) |
| Mise à jour biais | $b^{(l)} \leftarrow b^{(l)} - \eta \frac{\partial L}{\partial b^{(l)}}$ | Mise à jour des biais ($\eta$ = taux d’apprentissage) |
Exemple Numérique Concret
Prenons un réseau simple avec 2 entrées, 2 neurones cachés, et 1 sortie:
- Entrées : $x_1 = 0.5$, $x_2 = 0.8$
- Poids couche cachée : $W^{(1)} = \begin{pmatrix} 0.2 & 0.4 \ 0.6 & 0.3 \end{pmatrix}$
- Biais couche cachée : $b^{(1)} = \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix}$
- Valeur cible : $y_{target} = 0.9$
Propagation :
- Couche cachée
- $z_1^{(1)} = 0.2 \times 0.5 + 0.4 \times 0.8 + 0.1 = 0.52$
- $a_1^{(1)} = \sigma(0.52) = 0.6271$
- $z_2^{(1)} = 0.6 \times 0.5 + 0.3 \times 0.8 + 0.2 = 0.74$
- $a_2^{(1)} = \sigma(0.74) = 0.6770$
- Couche sortie :
- $z^{(2)} = 0.7 \times 0.6271 + 0.5 \times 0.6770 + 0.15 = 0.9275$
- $a^{(2)} = \sigma(0.9275) = 0.7166$
Rétropropagation :
-
Delta de sortie :
- $\frac{\partial L}{\partial a^{(2)}} = -(0.9 - 0.7166) = -0.1834$
- $\delta^{(2)} = -0.1834 \times 0.2031 = -0.0373$
-
Gradients biais de sortie :
- $\frac{\partial L}{\partial b^{(2)}} = \delta^{(2)} = -0.0373$
-
Deltas couche cachée :
- $\delta_1^{(1)} = -0.0261 \times 0.2338 = -0.0061$
- $\delta_2^{(1)} = -0.0186 \times 0.2187 = -0.0041$
-
Gradients biais cachés :
- $\frac{\partial L}{\partial b_1^{(1)}} = -0.0061$
- $\frac{\partial L}{\partial b_2^{(1)}} = -0.0041$
Pour vous aider a comprendre :
3.3 Test sur le problème XOR
Exercice 3.1 :
Maintenant que vous avez implémenté le réseau multicouches, testez-le sur le problème XOR :
def test_xor():
"""
Test du réseau multicouches sur le problème XOR
"""
# Données XOR
X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_xor = np.array([[0], [1], [1], [0]])
print("Test sur le problème XOR")
print("Données d'entrée :")
print(X_xor)
print("Sorties attendues :")
print(y_xor.flatten())
# TODO: Créer et entraîner le réseau
# Essayez différentes architectures
architectures = [
[2, 2, 1], # 2 entrées, 2 neurones cachés, 1 sortie
[2, 3, 1], # 2 entrées, 3 neurones cachés, 1 sortie
[2, 4, 1], # 2 entrées, 4 neurones cachés, 1 sortie
[2, 2, 2, 1], # 2 couches cachées
]
for arch in architectures:
print(f"\n--- Architecture {arch} ---")
# Créer et entraîner le réseau
mlp = PerceptronMultiCouches(arch, learning_rate=0.5, activation='sigmoid')
mlp.fit(X_xor, y_xor, epochs=1000, verbose=False)
# Test des prédictions
predictions = mlp.predict(X_xor)
print("Prédictions :")
for i in range(len(X_xor)):
print(f" {X_xor[i]} -> {predictions[i][0]:.4f} (attendu: {y_xor[i][0]})")
# Calculer l'accuracy
accuracy = mlp.compute_accuracy(y_xor, predictions)
print(f"Accuracy finale : {accuracy:.4f}")
# Lancer le test
test_xor()
Questions d’analyse :
- Le réseau arrive-t-il à résoudre XOR ? Avec quelle architecture minimale ?
- Comment le nombre de neurones cachés influence-t-il la convergence ?
- Que se passe-t-il avec plusieurs couches cachées ?
- L’initialisation des poids a-t-elle une influence ? (tester d’autres types d’initialisations)