Article Index

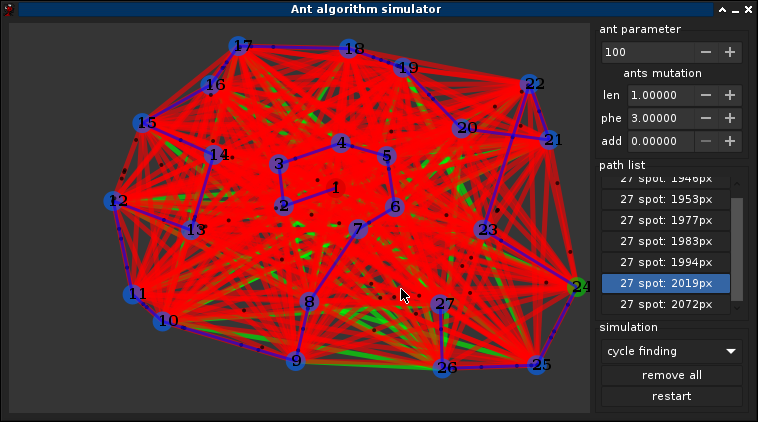
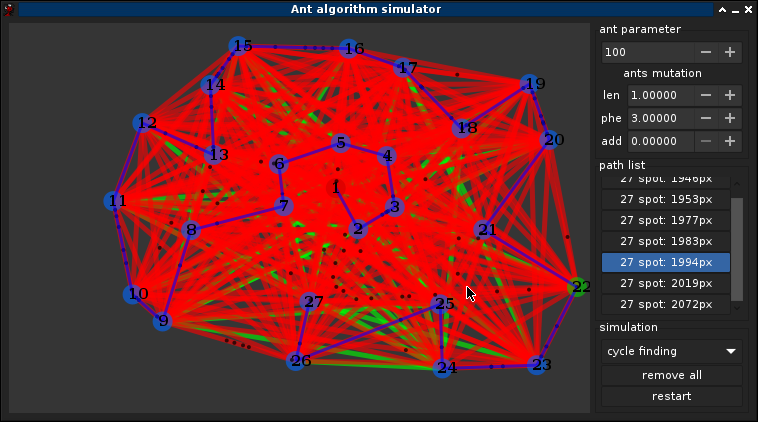
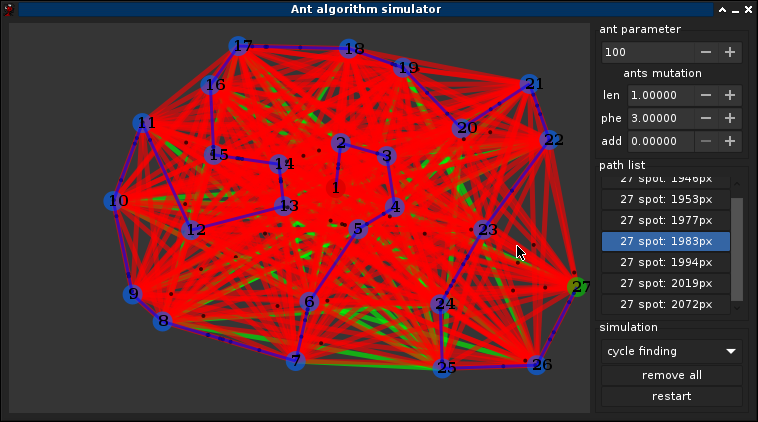
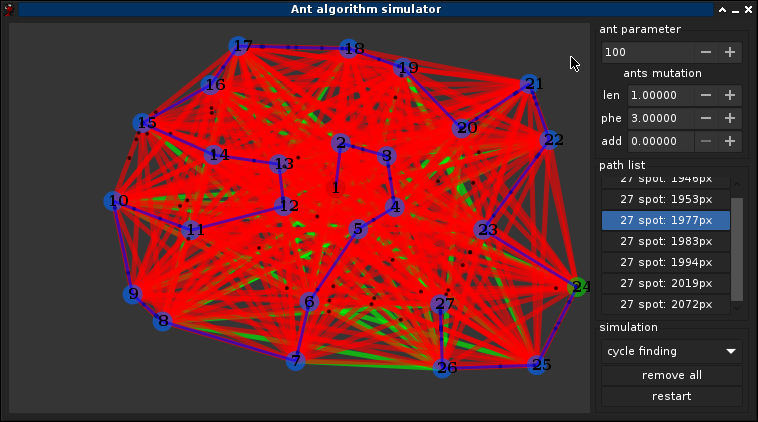
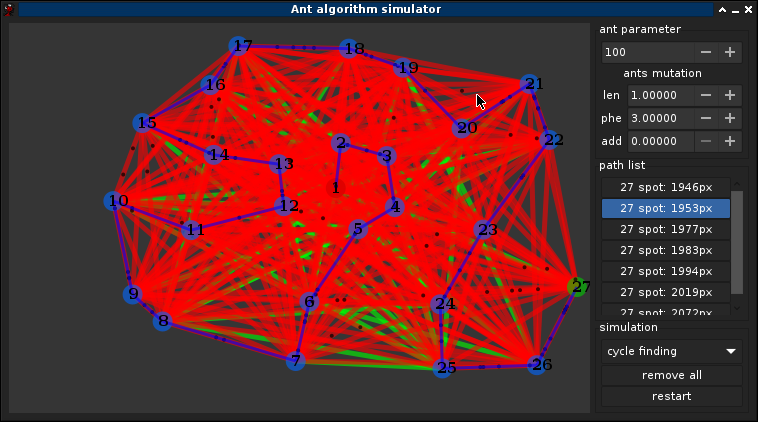
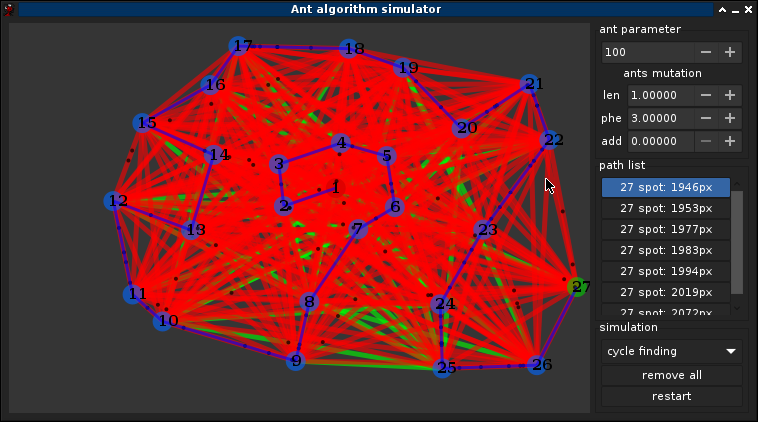
1.1°) Pourquoi les fourmis ?

Chaque individu de la colonie est à priori indépendant et n’est pas supervisé d’une manière ou d’une autre. Ce concept est appellé Hétérarchie (s’opposant à la Hiérarchie), chaque ndividu est aidé par la communauté dans son évolution et en retour il aide au bon fonctionnement de celle-ci. En observant une colonie de fourmis à la recherche de nourriture dans les environs du nid, on s’aperçoit qu’elle résoud des problèmes tels que celui de la recherche du plus court chemin. Les fourmis résolvent des problèmes complexes par des mécanismes assez simples a modéliser. Il est ainsi assez simple de simuler leur comportement par des algorithmes.

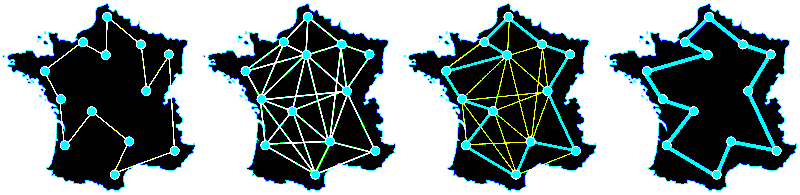
1.2°) Comportement des fourmis

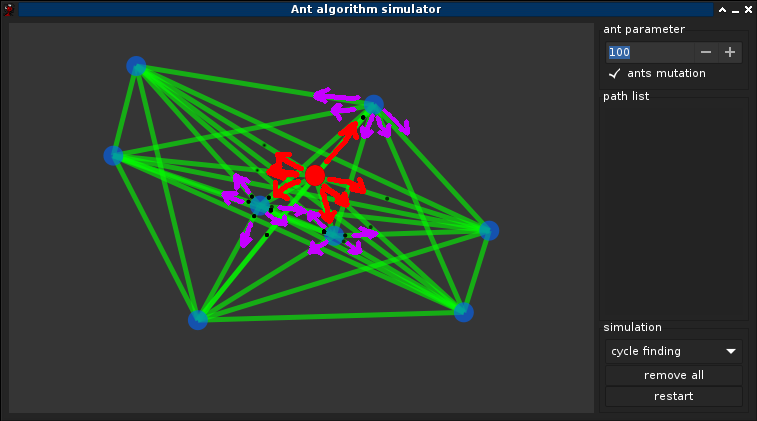
En marchant du nid à la source de nourriture (ce qui dans un premier temps se fait essentiellement de façon aléatoire), les fourmis déposent au passage sur le sol une substance odorante appelée phéromones. Cette substance permet ainsi donc de créer une piste chimique, sur laquelle les fourmis s’y retrouvent. Les phéromones ont un rôle de marqueur de chemin : quand les fourmis choisissent leur chemin, elles ont tendance à choisir la piste qui porte la plus forte concentration de phéromones. Ce comportement permet de trouver le chemin le plus court vers la nourriture lorsque les pistes de phéromones sont utilisées par la colonie entière. Autrement dit, lorsque plusieurs chemins marqués sont à la disposition d’une fourmi, cette dernière peut connaitre le chemin le plus court vers sa destination.

1.3°) Points communs algorithme/fourmis réel

Colonie d’individus coopérants : Comme pour les fourmis réelles, une colonie virtuelle est un ensemble d’entités non-synchronisés, qui se rassemblent ensemble pour trouver une "bonne" solution au problème considéré. Chaque groupe d’individus doit pouvoir trouver une solution même si elle est mauvaise.

Pistes de phéromones : Ces entités communiquent par le mécanisme des pistes de phéromone. Cette forme de communication joue un grand rôle dans le comportement des fourmis. Son rôle principal est de changer la manière dont l’environnement est perçu par les fourmis, en fonction de l’historique laissé par ces phéromones :

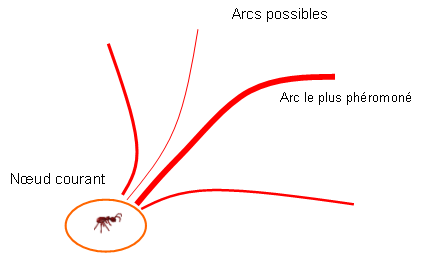
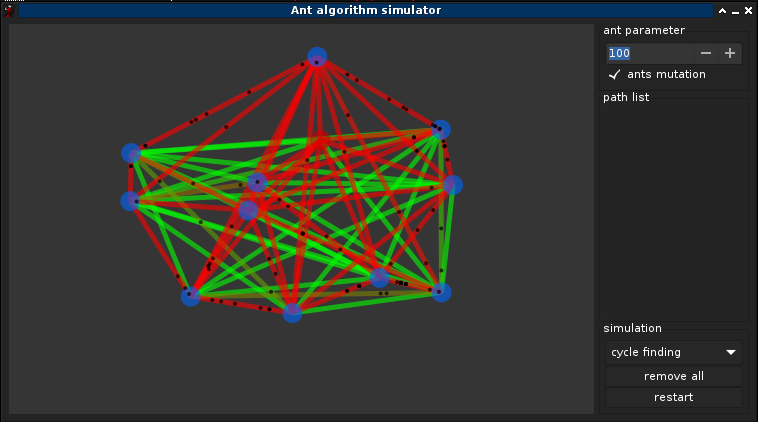
  • Évaporation des phéromones. La méta-heuristique ACO comprend aussi la possibilité d’évaporation des phéromones. Ce mécanisme permet d’oublier lentement ce qui s’est passé avant. C’est ainsi qu’elle peut diriger sa recherche vers de nouvelles directions, sans être trop contrainte par ses anciennes décisions.
  • Recherche du plus petit chemin. Les fourmis réelles et virtuelles partagent un but commun : recherche du plus court chemin reliant un point de départ (le nid) à des sites de destination (la nourriture). Cette algorithme peut également être utiliser par rechercher des cycle hamiltonien dans un graph plus ou moin complet.
  • Deplacement locaux. Les vraies fourmis ne sautent pas des cases, tout comme les fourmis virtuelles. Elles se contentent de se déplacer entre sites adjacents du terrain.
  • Choix aléatoire lors des transitions. Lorsqu’elles sont sur un site, les fourmis réelles et virtuelles doivent décider sur quel site adjacent se déplacer. Cette prise de décision se fait au hasard et dépend de l’information locale déposée sur le site courant. Elle doit tenir compte des pistes de phéromones, mais aussi du contexte de départ (ce qui revient à prendre en considération les données du problème d’optimisation combinatoire pour une fourmi virtuelle).

 


2.1°) Voyageur de commerce : Algorithm Ant System (AS)

La représentation d'une colonie de fourmie nécéssite de dissocier les éléments suivants:

  • des noeuds disposant d'une posiion spacial
  • des arcs reliant un niveaux de phéromone et une longuer (arriver/destination)
  • des fourmis avec une mémoire (noeud parcourus, paramètre aléatoire, …)

Le voyageur de commerce est un problème NP-complet. La méthaphore de la colonisation de fourmis s’y applique particulièrement bien. Ces caractéristique forme un graph (non orienter) et permete la recherche de circuit ou de “plus court chemain” suivant les caractéristiques du graphe. Le domaine d'étude seras limiter au graphs disposant d'une des propiétées suivante:

  • graphe complets (recherche de circuit hamiltonien le plus court : TSP)
  • graphe connecter (recherche de chemin élémentaire le plus court : )

2.2°) Conventions

la quantiter de phéromones et la longeurs des arcs influent sur le comportement aléatoire des fourmis suivent la formule:

  • $ω + \frac{phéromone^β}{length^α}$ (valeurs par défault : ω=0 ; α=1; β=3)
  • les fourmis ce déplace en cycle et parcours toutes un arcs par itération
  • le niveaux de phéromone est évaporé a la fin de chaque cycle
  • chaque fourmis à la mémoire du cycle (liste des noeuds et des arcs parcourus)
  • chaque fourmis vide ça mémoire à chaque nouveaux cycle

2.3°) Choix d'implémentation

  • Contrainte:
    • les fourmis doivent être indépendante, et sans synchronisation
  • Solution:
    • les fourmis ne ce déplace plus en terme de cycle mais en fonction du temps
    • les foumis déposes continuèlement une infime quantitées de phéromone
    • les phéromones s'évapores continuèlement en infime quantitées quand une fourmis passe
    • le premier parcourt suite une propagation homogène (répartition égale des fourmis)
    • les fourmis parte toutes du même noeud
  • Choix: Les arcs sont considéré comme des ensembles, on peut alors considéré des opération de base tel-que l'union, la disjonction, et la division qui permetron de distinguer
    • les arcs parcourus d'une fourmis
    • les arcs à parcourir au prochain “pas” pour un fourmis
    • les arcs restant
    • si la fourmis rentre dans un chemin impossible

2.4°) Fonctionement de l'algorithme

Si une fourmis ce déplace alors

    fourmis.déplacer(min(1, arcs.reste()));
    arcs.ajouter_pheromone();
    
sinon si (cherche_chemin et dernier(fourmi.chemin) = fourmi.cible) ou
         (cherche_cycle et taille(fourmi.chemin) = taille(ville)) alors

    si longueur(fourmi.chemin) <longeur(meilleur) alors
        meuilleur = fourmi.chemin;
    fin si
    evaporer(fourmi.chemin);
    fourmi.reinitialiser();

sinon

    # exclusion des arcs donc une des deux ville a déjà été parcourus
    arcs_disponible = connecter(fourmis);
    
    si taille(arcs_disponible) = 0 alors
        # le graph n'est pas complet
        fourmis.chemin.evaporer();
        fourmis.reinitialiser(mutation);
        fourmis = fourmis.suivante;
    fin si;
    
    fourmis.arcs_courent := distribution_discrete(
        random(), arcs_disponible,
        fourmis.tendance
        # tendance : calcule le poid de distribution de chaque arcs
        # en fonction des parametres ω;  α;  β de la fourmis actuelle
    );
    
    ajouter(fourmis.visiter, fourmis.cible);
    fourmis.cible := fourmis.arcs_courent.desitnation;

fin si;
Fourmis.reinitialiser() is
begin
    si system.mutation alors
        alpha := random(1..10);
        beta := random(1..10);
    fin si;
    
    gamma := system.facteur_aléatoire;
    chemin := vide();
    visitre := vide();
end ;     
arc.ajouter_pheromone(F : fourmis) is
begin
    // EVAPORATION_RATE = 0.001f
    level += 1.f / longuer(fourmis.arcs);
end ;
arc.evaporer() is
begin
    // EVAPORATION_RATE = 0.001f
    level *= 1.f - EVAPORATION_RATE;
end ;

 


3.1°) Choix des paramètres

rapelle ω = aléatoire, α influent sur la longeur, β influent sur les phéromones

  • lorsque le graph deviens trops grand (en nombre de noeud), et qu'il n'existe pas suffisament de fourmis pour avoire une convergence rapide vers une solution presque optimal alors ω premet d'augmenter le critère aléatoire sur le choix de l'arc, les fourmis peuvent donc empreinter plus souvent les arcs dont les phéromones et la longeurs sont normalement rejeter dans leurs contexte. ω doit être petit sinon la convergence n'apparait plus, bien que des solutions puissent émerger.
  • lorsque les noeuds du graph sont très éloigner alors α a moins d'importance, dans ce cas priviligier α avec un ratio supérieur idéalement 10/(plus petite longueur / plus grand longeur). Et inverssement à ω, β doit être petit si le nombre de fourmis est inssufisent par rapport au nombre de noeud idéalement β peut être choisit par 3*(nombre de fourmis) / (nombre de ville)

Ses choix n'ont pas été l'objet d'étude pousser, mais seulement le fruit de constatation lors des expériences.

3.2°) Optimisation

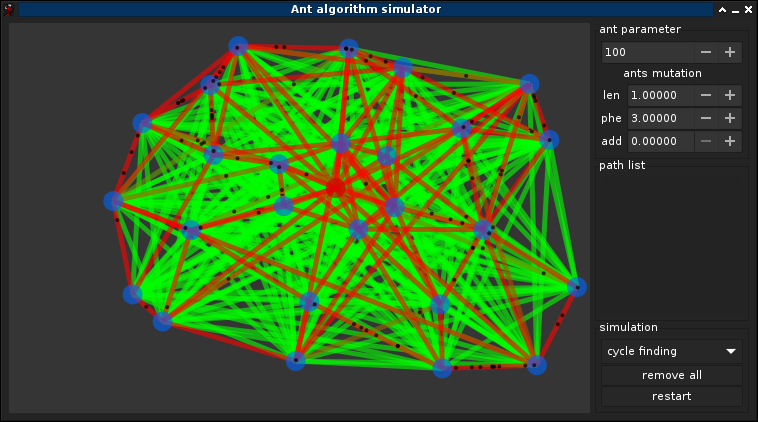
Mutation des fourmis ! Si ω,α,β sont dépendant du graphe, or le graph n'ai pas nécéssairement connue a l'avance donc l'idée est de tendre vers une solution optmimal de ω,α,β pendant la simulation, une méthode simple est avisagable:

  • valeurs par défault : ω=0 ; α=1; β=3
  • α et β prenne des valeurs aléatoires dans [0;10] quand
  • la fourmis ce perd (graph non complet) plus d'arc disponible
  • la fourmis trouve un cycle avec une longueur > au chemain actuel
  • ω ,α, β sont alors indépendants à chaque fourmis

cette solution simple montre après quelques teste, une convergance plus rapide vers une solution optimal (cf 6)

3.3°) Utilisation

  • Lors de la premiere itération toutes les fourmis sont répartie uniformement depuis la source, un ainsi de suite

  • Lorsque la propagation est terminer les niveaux de phéromone commence à apparaitre

  • Idem avec plus de villes et les paramètres ω;α;β fixes

Clic gauche Ajoute une ville
Clic droit sur un ville + déplacement Ajoute un arc entre deux ville
Clic gauche + majuscule Suprimme une ville
Clic droit + déplacement + majuscule Suprimme un arc
Clic gauche + control Ajoute une ville et des arcs vers chaque autres ville
Boutton “remove all” Supprimme toutes les villes et tous les arcs
Button “restart” Reinitialise les fourmis, phéromones
Molette souris vers le haut sur une ville Définie la source de propagation et lance la propagation si simulation = “cycle finding”
Molette souris vers le bas sur une ville Definie le point d'arriver pour la recherche de chemain (si simulation = “path finding”) et lance la simuluation dans ce cas
Ant parameter Definie la quantiter de fourmis
Ant mutation (actif)
  • Ajoute un critère aléatoire sur les parametres ω ,α, β
  • différentes pour chaque fourmis (cf: 3.2 optimisation)
Ant mutation (inactif) :
  • 3 parametre appaissent
  • Len = α ; Phe = β ; Add = ω

Source: svn://sleek-think.ovh/school/ant/

3.4°) Resultat expérimentaut

algorithme mise en oeuvre

acceptable trouver après meilleurs trouver après
9.54s 56.87s
4.21s 47.54s
25.23s 66.83s
34.88s 97.46s
15.80s 55.82s
20.90s 45.72s

Algorithme avec mutation

acceptable trouver après meilleurs trouver après
4.90s 40.31s
3.01s 70.04s
8.12s 22.20s
14.71s 100.53s
4.57s 62.44s
7.67s 58.29s

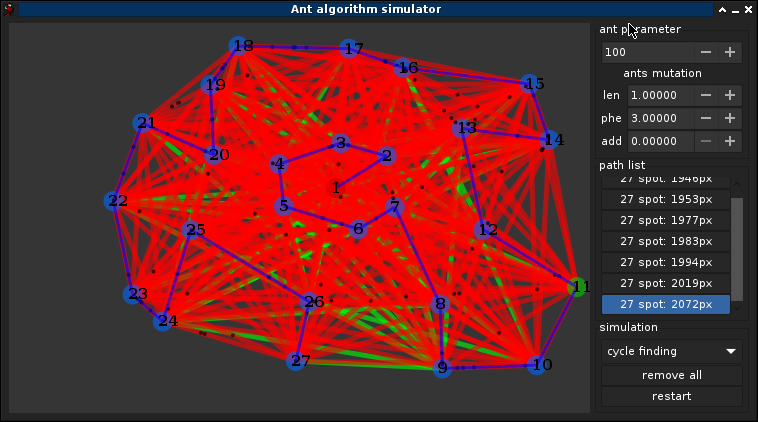
3.5°) Exemple complet

 

Pas d'autre solution trouver après (~40min) ont peut supposer que c'est une des meilleurs solutions, on peut également notifier que le graph ne change pas completements entre chaque itérations, les fourmis suivent toutes le chemin principale, le caractère aléatoire permet de trouver de fluctuer légèrement le chemin, bien quelles finissent par retrouver le chemin d'origine avec l'attirence des phéromones