Correction affine

Nous allons faire l'hypothèse que plus on se rapproche du sol, plus la distance de la correction affine initiale est grande. En revanche, à une distance supérieure ou égale à 5 mètres, la correction affine initiale est proche de quelques pixels (1-5), ce qui est suffisant pour prendre une matrice d'identité.

Calibration : Sur la base de cette hypothèse précédente, un étalonnage est effectué sur l'ensemble des données de l'échiquier. Nous détectons l'échiquier en utilisant la toolbox de calibration opencv sur chaque image spectrale à différentes hauteurs (de 1,6m à 5m). Ont s'aide de la fonction findChessboardCorners qui tente de déterminer si l'image d'entrée est une vue du motif d'échiquier et localise les coins internes de ce dernier. Les coordonnées détectées sont approximatives. Pour déterminer leurs positions avec précision, nous utilisons la fonction cornerSubPix comme expliqué dans la documentation :

for x in range(len(height)):
    h = height[x]
    S = SpectralImage()
    imgpoints = [None] * len(bands)

    for s,i in enumerate(bands):
        image = S.read_tiff(directory + h + str(i) + 'nm.tif')
        image = np.clip(image / image.max() * 255, 0, 255)
        image = image.astype('uint8')
        
        ret, corners = cv2.findChessboardCorners(image, chessboard_shape, None)
        if ret == True:
            corners2 = cv2.cornerSubPix(image, corners, chessboard_shape, (-1,-1), criteria)
            imgpoints[s] = corners2

Les données doivent être organisé puisque la détection du chessboard peut dans certain cas être "retourné" :

imgpoints = np.array(imgpoints)

for i in range(imgpoints.shape[0]):
    imgpoints[i] = imgpoints[i, np.argsort(imgpoints[i,:,0,0]), :, :]
    imgpoints[i] = imgpoints[i, np.argsort(imgpoints[i,:,0,1]), :, :]

np.save('data/' + h[0:-1] + '.npy', imgpoints)

Modèle linéaire : En utilisant tous les points détectés pour chaque bande spectrale, ont peu calculer un « grille centrale » (moyenne de chaque point). La transformée affine de chaque bande spectrale vers cette « grille centrale » est estimée. Théoriquement, la rotation et l'échelle ($A,B,C,D$) ne dépendent pas de la distance au sol, mais la translation ($X,Y$) oui. Les données extraites sont alors les suivantes et semble respecter notre assertion de départ :

Ainsi, un algorithme d'ajustement de courbe (Levenberg-Marquardt) avec régression linéaire des moindres carrés peut être utilisé pour ajuster une équation pour chaque bande spectrale par rapport à $X$ et $Y$ indépendamment vers cette « grille centrale ». Nous ajustons donc l'équation suivante $t = \alpha h^3 + \beta h^2 + \theta h + \gamma$ où $h$ est la hauteur, $t$ est la translation résultante et les facteurs $\alpha,\beta,\theta,\gamma$ sont les paramètres du modèle, ce qui correspond à la fonction $polynomial\_curve(x,a,b,c,d)$. Cela correspond plus spécifiquement au code suivant :

from scipy.optimize import curve_fit

def polynomial_curve(x, a, b, c, d):
    return a*x**3 + b*x**2 + c*x + d

# exemple pour l'ajustement de courbe entre $x$ et $h$
for i in range(all_transform_x.shape[1]):
    x, y = height, all_transform_x[:,i]
    popt, pcov = curve_fit(polynomial_curve, x, y)

Ont peu alors visualiser l'apprentissage de ces courbes en positionnant les points de détection et les courbes polynomial correspondantes :

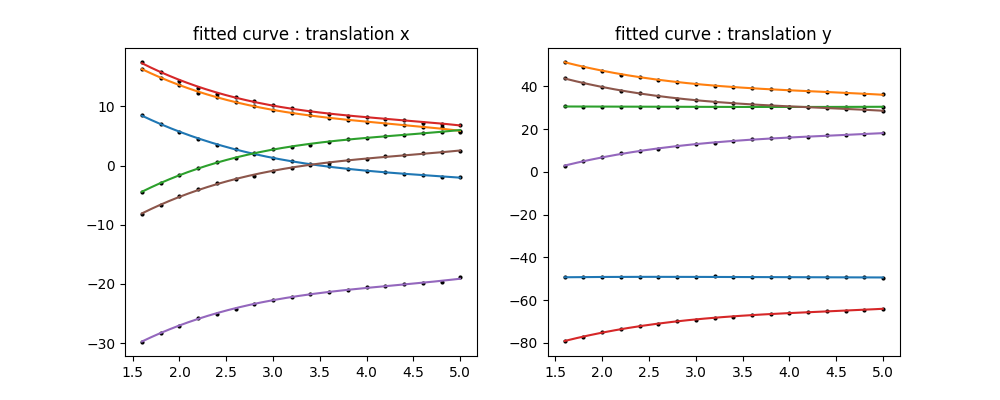
Correction : Sur la base du modèle estimé sur l'ensemble des données de l'échiquier, nous les transposons alors à l'ensemble des images de prairie. Pour effectuer la correction matricielle affine, nous utilisont les facteurs ($A,B,C,D$) de rotation et d'échelle à la hauteur la plus précise (1,6m la où la résolution spatiale de l'échiquier est la plus élevée), car elle ne dépend théoriquement pas de la hauteur. Pour la partie translation ($X,Y$), le modèle de courbe est appliqué pour chaque bande spectrale en utilisant la hauteur donnée fournie par le GPS de la caméra ! Chaque bande spectrale est déformée à l'aide de la transformation affine correspondante. Enfin, toutes les bandes spectrales sont recadrées à la limite minimale (translation minimale et maximale de chaque matrice affine). Cette première correction est une approximation du faite de l'imprécision du GPS. Elle fournit néhanmoins certaines propriétés spatiales que nous utiliserons lors de la deuxième étape !!

def affine_transform_linear(S, loaded):
    dsize = (loaded[0].shape[1], loaded[0].shape[0])
    transform = [None] * len(loaded)
        
    # best factor $a,b,c,d$ for each spectral band
    # extracted from the calibration
    rotation_scale = [(A,B,C,D) * len(bands)]

    # idem for $alpha,beta,gamma,psi$ on each spectral band
    translation_model_params = [(X_params,Y_params) * len(bands)]
    
    for i in range(len(loaded)):
        x = polynomial_curve(S.height, *translation_model_params[i][0])
        y = polynomial_curve(S.height, *translation_model_params[i][1])
        transform[i] = np.array([
            [rotation_scale[i][0], rotation_scale[i][1], x],
            [rotation_scale[i][2], rotation_scale[i][3], y],
        ])
        loaded[i] = cv2.warpAffine(loaded[i], transform[i], dsize)

    return loaded, np.array(transform)

Résultat affine