Correction perspective
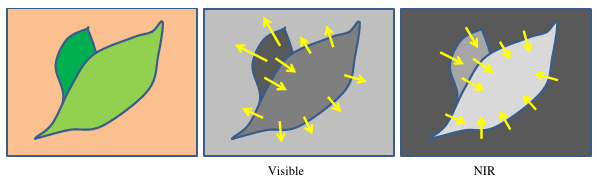
Chaque bande spectrale a des propriétés et des valeurs différentes par nature, mais nous pouvons essayer d'extraire des similaritées en transformant chaque bande spectrale vers une dérivée absolue, pour trouver des similarités dans la rupture des gradients entre elles et tout particulièrement sur les bordures des feuilles ! Comme nous pouvons le voir sur la figure suivante, les gradients peuvent avoir des directions opposées selon les bandes spectrales, ce qui fait de la dérivée absolue une étape importante pour la correspondance entre les différentes bandes spectrales. Passer l'information en absolue permet d'obtenir des gradient dans le "même" sens.
La correction affine permet de faciliter la recherche et la mise en correspondance de points-clé en ajoutant les propriétés des lignes épipolaires (proche). Ainsi, la correspondance de points-clé extraits peut être spatialement délimitée car nous savons que :
- la translation entre deux point-clés est limitée à quelques pixels (moins de 10px grâce à la correction affine)
- l'angle entre deux point-clés est limité à $[-1,1]$ degré (la rotation est infime)
- idem pour la mise à l'échelle qui est proche de zero
Calcule des gradients : Pour calculer le gradient de l'image avec un impact minimal de la distribution lumineuse (bruit, ombre, réflectance, spéculaire, ...), chaque bande spectrale est normalisée en utilisant le flou gaussien, la taille du noyau est fixé empiriquement à 19 et les images normalisées finales sont définies par $I/(G+1)*255$ où $I$ est la bande spectrale et $G$ est le flou gaussien de ces bandes spectrales. Cette première étape permet de minimiser l'impact du bruit sur le gradient et de lisser le signal en cas de forte réflectance. En utilisant cette image normalisée, le gradient $I_{grad}(x,y)$ est calculé avec la somme absolue des filtres de Sharr pour la dérivée horizontale $S_x$ et verticale $S_y$, notée $I_{grad}(x,y)=\frac{1}{2}|S_x|+\frac{1}{2}|S_y|$. Enfin, tous les gradients $I_{grad}(x,y)$ sont normalisés à l'aide de CLAHE pour améliorer localement leur intensité et augmenter le nombre de points clés détectés. Ont transpose donc tout cela en code python :
def build_gradient(img, scale = 0.15, delta=0):
clahe = cv2.createCLAHE(clipLimit=1.0, tileGridSize=(8,8))
grad_x = cv2.Scharr(img, cv2.CV_32F, 1, 0, scale=scale, delta=delta, borderType=cv2.BORDER_DEFAULT)
grad_y = cv2.Scharr(img, cv2.CV_32F, 0, 1, scale=scale, delta=delta, borderType=cv2.BORDER_DEFAULT)
abs_grad_x = cv2.convertScaleAbs(grad_x)
abs_grad_y = cv2.convertScaleAbs(grad_y)
grad = cv2.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0)
grad = cv2.convertScaleAbs(grad)
grad = grad.astype('float')**2
grad = grad/grad.max()*255
grad = grad.reshape([*grad.shape, 1])
grad = grad.astype('uint8')
grad = clahe.apply(grad)
return grad.astype('uint8')Extracteur de points clé : Un point clé est un point d'intérêt. Il définit ce qui est important et distinctif dans une image (coins, bords, etc.). Différents types d'extracteurs de points clés ont été testé. Ces algorithmes sont largement décrits dans de multiples études, ils sont tous disponibles et facilement utilisables grâce à OpenCV. Nous allons donc les étudiées en faisant varier les paramètres les plus influents pour chacune d'entre elles avec trois modalités :
| Abrv | paramètre | modalité 1 | modalité 2 | modalité 3 |
| ORB | nfeatures | 5000 | 10000 | 15000 |
| AKAZE | nOctaves, nOctaveLayers | (1, 1) | (2, 1) | (2, 2) |
| KAZE | nOctaves, nOctaveLayers | (4, 2) | (4, 4) | (2, 2) |
| BRISK | nOctaves, nOctaveLayers | (0, 0.1) | (1, 0.1) | (2, 0.1) |
| AGAST | threshold | 71 | 92 | 163 |
| MSER | None | None | None | None |
| SURF | nOctaves, nOctaveLayers | (1, 1) | (2, 1) | (2, 2) |
| FAST | threshold | 71 | 92 | 163 |
| GFTT | maxCorners | 5000 | 10000 | 15000 |
def keypoint_detect(img1, img2, method='GFTT'):
# dictionnaire contenant les différent algos
# cf tableau précédent
detectors = {'ORB' : None}
# construction du detecteur de point clé
detector = detectors[method]()
# detection des points clé
kp1, kp2 = detector.detect([img1, img2],None)
# construction du modél d'extraction de propriété
descriptor = cv2.ORB_create()
# extraction de proriété par point-clé
(kp1, kp2), (des1, des2) = descriptor.compute([img1, img2], [kp1, kp2])
# association par bruteforce (toute les combinaisons)
bf = cv2.BFMatcher(descriptor.defaultNorm(), crossCheck=True)
# association
matches = bf.match(des1,des2)
return matches, kp1, kp2
Détection de point clé : Nous utilisons un des extracteurs de points clés mentionnés ci-dessus entre chaque gradient de bande spectrale (tous les extracteurs sont évalués). Pour chaque point clé détecté, nous extrayons un descripteur en utilisant le descripteur de texture de ORB. Nous faisons correspondre tous les points clés détectés vers la bande spectrale de référence (toutes les bandes sont évaluées). Toutes les correspondances sont filtrées par distance, position et l'angle, afin d'éliminer la majorité des faux positifs le long des lignes épipolaires correspondantes. Enfin, nous utilisons la fonction findHomography entre les points clés détectés/filtrés avec le RANSAC, pour déterminer le meilleur sous-ensemble de correspondances afin de calculer la correction de perspective.
def refine_allignement(loaded, method='SURF', ref=1, verbose=True):
img = [ i.astype('float32') for i in loaded]
img = [ gradient_normalize(i) for i in img]
grad = [ build_gradient(i).astype('uint8') for i in img]
img = [ (i/i.max()*255).astype('uint8') for i in img]
# identify transformation for each band to the next one
dsize = (loaded[0].shape[1], loaded[0].shape[0])
bbox, centers, keypoint_found = [], [], []
max_dist = 10
for i in range(0, len(loaded)):
if i == ref:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
matches, kp1, kp2 = keypoint_detect(grad[ref], grad[i], method)
matches = keypoint_filter(matches, kp1, kp2, max_dist)
if len(matches) < 2:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
source = np.array([kp1[i.queryIdx].pt for i in matches], dtype=float)
target = np.array([kp2[i.trainIdx].pt for i in matches], dtype=float)
matches = [cv2.DMatch(i,i,0) for i in range(len(source))]
source = source[np.newaxis, :].astype('int')
target = target[np.newaxis, :].astype('int')
M, mask = cv2.findHomography(target, source, cv2.RANSAC)
if M is None:
keypoint_found.append(-1)
centers.append(np.array([0,0]))
continue
loaded[i] = cv2.warpPerspective(loaded[i], M, dsize)
bbox.append(get_perspective_min_bbox(M, loaded[ref]))
center = np.array(dsize)/2
centers.append(cv2.perspectiveTransform(np.array([[center]]),M)[0,0] - center)
mask = np.where(mask.flatten())
target = np.float32(target[0,mask,:])
source = np.float32(source[0,mask,:])
keypoint_found.append(len(mask[0]))
return loaded, np.array(bbox), keypoint_found, np.array(centers)Correction : La correction de perspective entre chaque bande spectrale et la référence est estimée et appliquée. Enfin, toutes les bandes spectrales sont recadrées à la limite minimale, obtenue en appliquant une transformation de perspective à chaque coin de l'image (plus un offset $p$) :
def get_perspective_min_bbox(M, img, p=2):
h,w = img.shape[:2]
pts_x = np.float32([[ p, p], [ p, h-p]]).reshape(-1,1,2)
pts_y = np.float32([[w-p,h-p], [w-p, p]]).reshape(-1,1,2)
coords_x = cv2.perspectiveTransform(pts_x,M)[:,0,:]
coords_y = cv2.perspectiveTransform(pts_y,M)[:,0,:]
[xmin, xmax] = max(coords_x[0,0], coords_x[1,0]), min(coords_y[0,0], coords_y[1,0])
[ymin, ymax] = max(coords_x[0,1], coords_y[1,1]), min(coords_x[1,1], coords_y[0,1])
return np.int32([ymin,xmin,ymax,xmax])
Résultat Perspective
